题目内容
给定直线l:y=2x-16,抛物线C：y2=ax(a>0).
(1)当抛物线C的焦点在直线l上时，确定抛物线C的方程；
(2)若△ABC的三个顶点都在(1)所确定的抛物线C上，且点A的纵坐标ya=8,△ABC的重心恰在抛物线C的焦点上，求直线BC的方程.
(1)当抛物线C的焦点在直线l上时，确定抛物线C的方程；
(2)若△ABC的三个顶点都在(1)所确定的抛物线C上，且点A的纵坐标ya=8,△ABC的重心恰在抛物线C的焦点上，求直线BC的方程.
BC的直线方程为y+4=-4(x-11),即4x+y-40=0.
(1)∵抛物线的焦点为(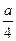
,0),代入y=2x-16,得a=32.
∴抛物线方程为y2=32x.
(2)∵yA=8,∴xA=2.
∵F(8,0)为△ABC的重心，∴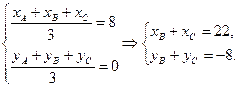
又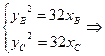
(yB+yC)(yB-yC)=32(xB-xC)
=-4=kBC,
又中线AF与BC交点坐标x=
=11,y=
=
=-4,
∴BC的直线方程为y+4=-4(x-11),即4x+y-40=0.
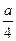,0),代入y=2x-16,得a=32.∴抛物线方程为y2=32x.
(2)∵yA=8,∴xA=2.
∵F(8,0)为△ABC的重心，∴
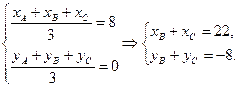
又
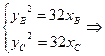(yB+yC)(yB-yC)=32(xB-xC)=-4=kBC,又中线AF与BC交点坐标x=
=11,y===-4,∴BC的直线方程为y+4=-4(x-11),即4x+y-40=0.
练习册系列答案
相关题目
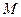为抛物线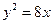
上一动点,F为抛物线的焦点,定点
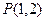,则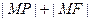
的最小值为( )
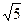C.6 D.5
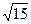，求抛物线方程.
)
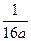