题目内容
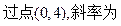 -1的直线与抛物线
-1的直线与抛物线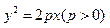 交于两点A,B,如果
交于两点A,B,如果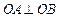 (O为原点)求P的值及抛物线的焦点坐标。
(O为原点)求P的值及抛物线的焦点坐标。p=2.;抛物线方程为y2=4x,焦点坐标为F(1,0).
直线方程为y=-x+4,联立方程 ,消去y得,
,消去y得,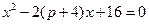 .
.
设A( ),B(
),B( ),得
),得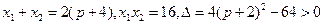
所以: ,p>0.
,p>0.
由已知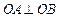 可得
可得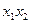 +
+ =0,从而16-8p=0,得p=2.
=0,从而16-8p=0,得p=2.
所以抛物线方程为y2=4x,焦点坐标为F(1,0).
 ,消去y得,
,消去y得,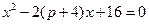 .
.设A(
 ),B(
),B( ),得
),得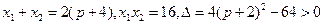
所以:
 ,p>0.
,p>0.由已知
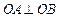 可得
可得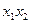 +
+ =0,从而16-8p=0,得p=2.
=0,从而16-8p=0,得p=2.所以抛物线方程为y2=4x,焦点坐标为F(1,0).

练习册系列答案
相关题目
 直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.
直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.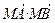 的取值范围;
的取值范围;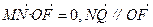 ;
;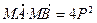 ,△ABN的面积的取值范围为[5
,△ABN的面积的取值范围为[5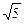 ,20
,20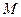 为抛物线
为抛物线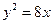 上一动点,F为抛物线的焦点,定点
上一动点,F为抛物线的焦点,定点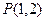 ,则
,则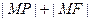 的最小值为( )
的最小值为( )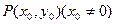 的切线方程为
的切线方程为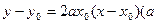 为常数).
为常数).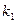 的直线PA与抛物线的另一交点为A,斜率为
的直线PA与抛物线的另一交点为A,斜率为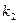 的直线PB与抛物线的另一交点为B(A、B两点不同),且满足
的直线PB与抛物线的另一交点为B(A、B两点不同),且满足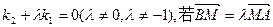 ,求证线段PM的中点在y轴上;
,求证线段PM的中点在y轴上;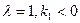 时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围.
时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围. 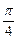 的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积.
的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积.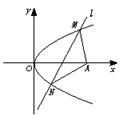
 C.6 D.5
C.6 D.5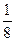
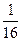
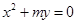 上的点到定点
上的点到定点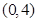 和到定直线
和到定直线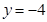 的距离相等,
的距离相等,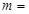 ( )
( )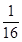 ;
;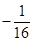 ;
;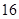 ;
;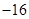 .
.