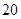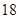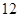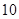题目内容
已知圆C:(x-4)2+(y-m)2=16(m∈N*),直线4x-3y-16=0过椭圆E: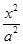 +
+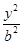 =1(a>b>0)的右焦点,且被圆C所截得的弦长为
=1(a>b>0)的右焦点,且被圆C所截得的弦长为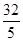 ,点A(3,1)在椭圆E上.
,点A(3,1)在椭圆E上.
(1)求m的值及椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求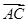 ·
· 的取值范围.
的取值范围.
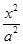 +
+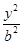 =1(a>b>0)的右焦点,且被圆C所截得的弦长为
=1(a>b>0)的右焦点,且被圆C所截得的弦长为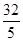 ,点A(3,1)在椭圆E上.
,点A(3,1)在椭圆E上.(1)求m的值及椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求
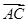 ·
· 的取值范围.
的取值范围.(1)m=4  +
+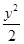 =1
=1
(2)[-12,0]
 +
+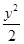 =1
=1(2)[-12,0]
(1)因为直线4x-3y-16=0被圆C所截得的弦长为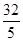 ,所以圆心C(4,m)到直线4x-3y-16=0的距离为
,所以圆心C(4,m)到直线4x-3y-16=0的距离为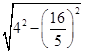 =
= ,
,
即 =
= ,解得m=4或m=-4(舍去).
,解得m=4或m=-4(舍去).
又直线4x-3y-16=0过椭圆E的右焦点,所以椭圆E的右焦点F2的坐标为(4,0),则其左焦点F1的坐标为(-4,0).
因为椭圆E过A点,所以|AF1|+|AF2|=2a,
所以2a=5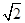 +
+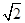 =6
=6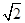 ,所以a=3
,所以a=3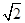 ,a2=18,b2=2,
,a2=18,b2=2,
故椭圆E的方程为 +
+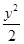 =1.
=1.
(2)由(1)知C(4,4),又A(3,1),所以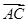 =(1,3),设Q(x,y),则
=(1,3),设Q(x,y),则 =(x-3,y-1),则
=(x-3,y-1),则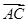 ·
· =x+3y-6.令x+3y=n,
=x+3y-6.令x+3y=n,
则由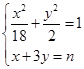 ,消去x得18y2-6ny+n2-18=0.
,消去x得18y2-6ny+n2-18=0.
因为直线x+3y=n与椭圆E有公共点,
所以Δ=(-6n)2-4×18×(n2-18)≥0,
解得-6≤n≤6,故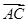 ·
· =x+3y-6的取值范围为[-12,0].
=x+3y-6的取值范围为[-12,0].
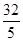 ,所以圆心C(4,m)到直线4x-3y-16=0的距离为
,所以圆心C(4,m)到直线4x-3y-16=0的距离为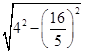 =
= ,
,即
 =
= ,解得m=4或m=-4(舍去).
,解得m=4或m=-4(舍去).又直线4x-3y-16=0过椭圆E的右焦点,所以椭圆E的右焦点F2的坐标为(4,0),则其左焦点F1的坐标为(-4,0).
因为椭圆E过A点,所以|AF1|+|AF2|=2a,
所以2a=5
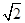 +
+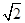 =6
=6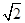 ,所以a=3
,所以a=3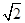 ,a2=18,b2=2,
,a2=18,b2=2,故椭圆E的方程为
 +
+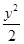 =1.
=1.(2)由(1)知C(4,4),又A(3,1),所以
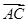 =(1,3),设Q(x,y),则
=(1,3),设Q(x,y),则 =(x-3,y-1),则
=(x-3,y-1),则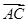 ·
· =x+3y-6.令x+3y=n,
=x+3y-6.令x+3y=n,则由
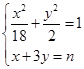 ,消去x得18y2-6ny+n2-18=0.
,消去x得18y2-6ny+n2-18=0.因为直线x+3y=n与椭圆E有公共点,
所以Δ=(-6n)2-4×18×(n2-18)≥0,
解得-6≤n≤6,故
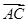 ·
· =x+3y-6的取值范围为[-12,0].
=x+3y-6的取值范围为[-12,0].
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
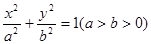 的左、右顶点分别是
的左、右顶点分别是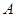 、
、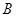 ,左、右焦点分别是
,左、右焦点分别是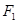 、
、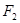 .若
.若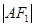 ,
,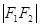 ,
,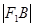 成等比数列,求此椭圆的离心率.
成等比数列,求此椭圆的离心率.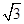 ,0),椭圆
,0),椭圆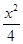 +y2=1与直线y=k(x+
+y2=1与直线y=k(x+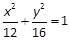 ,则以点
,则以点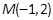 为中点的弦所在直线方程为( ).
为中点的弦所在直线方程为( ).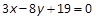
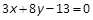
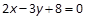
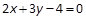
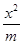 +
+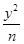 =1与双曲线
=1与双曲线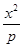 -
-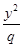 =1(m,n,p,q均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则
=1(m,n,p,q均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则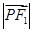 ·
·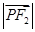 =( )
=( )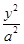 +
+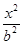 =1(a>b>0)的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A,B两点,已知A(
=1(a>b>0)的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A,B两点,已知A(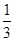 ,
,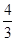 ).
).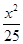 +
+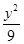 =1的左、右焦点分别是F1、F2,P为椭圆C上的一点,且PF1⊥PF2,则△PF1F2的面积为________.
=1的左、右焦点分别是F1、F2,P为椭圆C上的一点,且PF1⊥PF2,则△PF1F2的面积为________.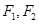 为椭圆
为椭圆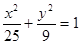 的两个焦点,过
的两个焦点,过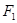 的直线交椭圆于两点,
的直线交椭圆于两点,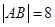 ,
,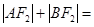 ( )
( )