题目内容
已知点M(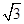 ,0),椭圆
,0),椭圆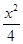 +y2=1与直线y=k(x+
+y2=1与直线y=k(x+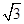 )交于点A、B,则△ABM的周长为( )
)交于点A、B,则△ABM的周长为( )
A.4 B.8 C.12 D.16
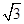 ,0),椭圆
,0),椭圆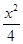 +y2=1与直线y=k(x+
+y2=1与直线y=k(x+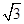 )交于点A、B,则△ABM的周长为( )
)交于点A、B,则△ABM的周长为( )A.4 B.8 C.12 D.16
B
因为直线过椭圆的左焦点(-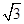 ,0),所以△ABM的周长为|AB|+|AM|+|BM|=4a=8,故选B.
,0),所以△ABM的周长为|AB|+|AM|+|BM|=4a=8,故选B.
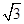 ,0),所以△ABM的周长为|AB|+|AM|+|BM|=4a=8,故选B.
,0),所以△ABM的周长为|AB|+|AM|+|BM|=4a=8,故选B.
练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 (a>b>0)经过D(2,0),E(1,
(a>b>0)经过D(2,0),E(1, )两点.
)两点.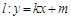 与椭圆Γ交于不同两点A,B,点G是线段AB中点,点O是坐标原点,设射线OG交Γ于点Q,且
与椭圆Γ交于不同两点A,B,点G是线段AB中点,点O是坐标原点,设射线OG交Γ于点Q,且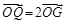 .
.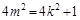
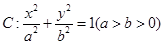 的左右焦点为
的左右焦点为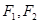 ,上顶点为
,上顶点为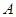 ,点
,点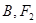 关于
关于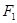 对称,且
对称,且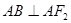
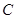 的离心率;
的离心率;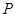 是过
是过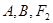 三点的圆上的点,若
三点的圆上的点,若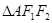 的面积为
的面积为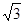 ,求点
,求点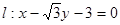 距离的最大值。
距离的最大值。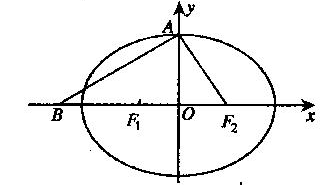
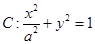 经过点
经过点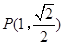 .
.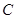 的方程及其离心率;
的方程及其离心率;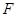 的直线(不经过点
的直线(不经过点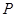 )与椭圆交于
)与椭圆交于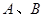 两点,当
两点,当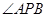 的平分线为
的平分线为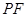 时,求直线
时,求直线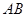 的斜率
的斜率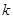 .
.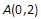 ,右焦点F与点
,右焦点F与点 的距离为2。
的距离为2。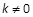 的直线
的直线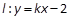 与椭圆相交于不同的两点M,N满足
与椭圆相交于不同的两点M,N满足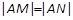 ,求直线l的方程。
,求直线l的方程。
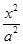 +
+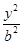 =1(a>b>0)的右焦点,且被圆C所截得的弦长为
=1(a>b>0)的右焦点,且被圆C所截得的弦长为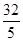 ,点A(3,1)在椭圆E上.
,点A(3,1)在椭圆E上.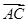 ·
· 的取值范围.
的取值范围.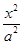 +
+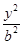 =1(a>b>0)的两顶点为A(a,0),B(0,b),且左焦点为F,△FAB是以角B为直角的直角三角形,则椭圆的离心率e为( )
=1(a>b>0)的两顶点为A(a,0),B(0,b),且左焦点为F,△FAB是以角B为直角的直角三角形,则椭圆的离心率e为( )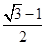
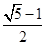
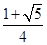
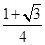
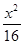 +
+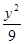 =1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
=1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )