题目内容
设椭圆E: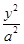 +
+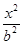 =1(a>b>0)的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A,B两点,已知A(
=1(a>b>0)的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A,B两点,已知A(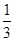 ,
,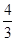 ).
).
(1)求椭圆E的方程;
(2)设点C是椭圆E上到直线PF1距离最远的点,求C点的坐标.
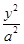 +
+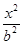 =1(a>b>0)的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A,B两点,已知A(
=1(a>b>0)的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A,B两点,已知A(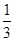 ,
,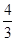 ).
).(1)求椭圆E的方程;
(2)设点C是椭圆E上到直线PF1距离最远的点,求C点的坐标.
(1) +x2=1 (2)(
+x2=1 (2)(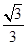 ,-
,-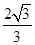 )
)
 +x2=1 (2)(
+x2=1 (2)(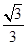 ,-
,-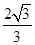 )
)(1)由A(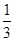 ,
,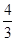 )和P(3,4)可求直线PF1的方程为y=x+1.
)和P(3,4)可求直线PF1的方程为y=x+1.
令x=0,得y=1,即c=1.
椭圆E的焦点为F1(0,1),F2(0,-1),由椭圆的定义可知.
2a=|AF1|+|AF2|
= +=2
+=2 .
.
∴a= ,b=1,
,b=1,
所以椭圆E的方程为 +x2=1.
+x2=1.
(2)设与直线PF1平行的直线l:y=x+m.
 ,消去y得3x2+2mx+m2-2=0,
,消去y得3x2+2mx+m2-2=0,
Δ=(2m)2-4×3×(m2-2)=0,
即m2=3,∴m=±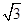 .
.
要使点C到直线PF1的距离最远,则直线l要在直线PF1的下方,所以m=-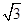 .
.
此时直线l与椭圆E的切点坐标为(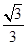 ,-
,-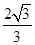 ),故C(
),故C(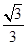 ,-
,-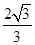 )即为所求.
)即为所求.
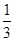 ,
,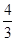 )和P(3,4)可求直线PF1的方程为y=x+1.
)和P(3,4)可求直线PF1的方程为y=x+1.令x=0,得y=1,即c=1.
椭圆E的焦点为F1(0,1),F2(0,-1),由椭圆的定义可知.
2a=|AF1|+|AF2|
=
 +=2
+=2 .
.∴a=
 ,b=1,
,b=1,所以椭圆E的方程为
 +x2=1.
+x2=1.(2)设与直线PF1平行的直线l:y=x+m.
 ,消去y得3x2+2mx+m2-2=0,
,消去y得3x2+2mx+m2-2=0,Δ=(2m)2-4×3×(m2-2)=0,
即m2=3,∴m=±
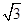 .
.要使点C到直线PF1的距离最远,则直线l要在直线PF1的下方,所以m=-
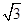 .
.此时直线l与椭圆E的切点坐标为(
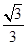 ,-
,-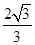 ),故C(
),故C(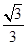 ,-
,-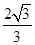 )即为所求.
)即为所求.
练习册系列答案
相关题目
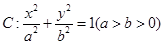 的左右焦点为
的左右焦点为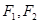 ,上顶点为
,上顶点为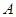 ,点
,点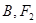 关于
关于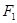 对称,且
对称,且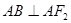
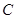 的离心率;
的离心率;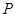 是过
是过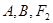 三点的圆上的点,若
三点的圆上的点,若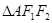 的面积为
的面积为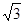 ,求点
,求点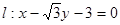 距离的最大值。
距离的最大值。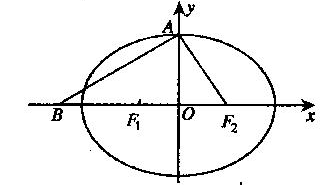
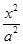 +
+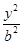 =1(a>b>0)的右焦点,且被圆C所截得的弦长为
=1(a>b>0)的右焦点,且被圆C所截得的弦长为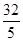 ,点A(3,1)在椭圆E上.
,点A(3,1)在椭圆E上.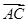 ·
· 的取值范围.
的取值范围.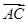 =2
=2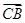 ,则点C的轨迹是( )
,则点C的轨迹是( )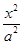 +
+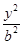 =1(a>b>0)的两顶点为A(a,0),B(0,b),且左焦点为F,△FAB是以角B为直角的直角三角形,则椭圆的离心率e为( )
=1(a>b>0)的两顶点为A(a,0),B(0,b),且左焦点为F,△FAB是以角B为直角的直角三角形,则椭圆的离心率e为( )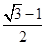
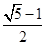
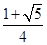
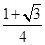
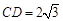 ,
,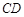 的中点为
的中点为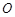 ,动点
,动点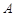 满足
满足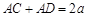 (
(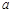 为正常数).
为正常数).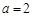 ,动点
,动点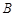 满足
满足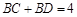 ,且
,且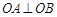 ,试求
,试求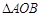 面积的最大值和最小值.
面积的最大值和最小值.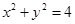 的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).
的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).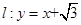 交于A,B两点,若
交于A,B两点,若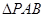 的面积为2,求C的标准方程.
的面积为2,求C的标准方程.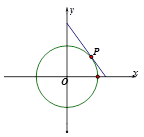
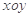 中,已知椭圆
中,已知椭圆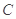 ∶
∶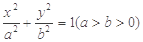 的左、右焦点分别
的左、右焦点分别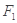 、
、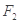 焦距为
焦距为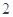 ,且与双曲线
,且与双曲线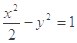 共顶点.
共顶点.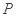 为椭圆
为椭圆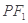 交椭圆
交椭圆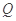 .
.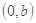 ,求过
,求过
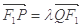 ,且
,且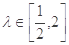 ,求
,求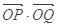 的最大值.
的最大值.