题目内容

若一动点M与定直线l：x=
16
5
及定点A（5，0）的距离比是4：5．
（1）求动点M的轨迹C的方程；
（2）设所求轨迹C上有点P与两定点A和B（-5，0）的连线互相垂直，求|PA|•|PB|的值．
（1）设动点M（x，y），
根据题意得
|x-
16
5
|
(x-5)2+y2
=
4
5
，
化简得9x2-16y2=144，
即
x2
16
-
y2
9
=1．
（2）由（1）知轨迹C为双曲线，A、B即为C的两个焦点，
∴|PA|-|PB|=±8．①
又PA⊥PB，∴|PA|2+|PB|2=|AB|2=100．②
由②-①2得|PA|•|PB|=18．
练习册系列答案
相关题目
已知椭圆Γ：(a＞b＞0)经过D(2，0)，E(1，)两点.
(1)求椭圆Γ的方程；
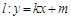(2)若直线与椭圆Γ交于不同两点A，B，点G是线段AB中点，点O是坐标原点，设射线OG交Γ于点Q，且.
①证明：
②求△AOB的面积.
如图，在平行四边形OABC中，点O是原点，点A和点C的坐标分别是（3，0）、（1，3），点D是线段AB上的动点．
（1）求AB所在直线的一般式方程；
（2）当D在线段AB上运动时，求线段CD的中点M的轨迹方程．
在同一直角坐标系中，经过伸缩变换
x′=5x
y′=3y
后，曲线C变为曲线x′2+y′2=1，则曲线C的方程为（　　）
A．25x2+9y2=1B．9x2+25y2=1C．25x+9y=1D．
x2
25
+
y2
9
=1
已知双曲线
x2
2
-y2=1的左、右顶点分别为A1，A2，点P（x1，y1），Q（x1，-y1）是双曲线上不同的两个动点．
（1）求直线A1P与A2Q交点的轨迹E的方程；
（2）若过点H（0，h）（h＞1）的两条直线l1和l2与轨迹E都只有一个交点，且l1⊥l2，求h的值．
在圆x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足．当点P在圆上运动时，线段PD的中点M的轨迹是（　　）
A．椭圆B．双曲线C．抛物线D．圆
点M与点F（3，0）的距离比它到直线x+1=0的距离多2，则点M的轨迹方程为______．
已知直线l：y=mx+1与曲线C：ax2+y2=2（m、a∈R）交于A、B两点，O为坐标原点．
（1）当m=0时，有∠AOB=
π
3
，求曲线C的方程；
（2）当实数a为何值时，对任意m∈R，都有
OA
•
OB
为定值T？指出T的值；
（3）已知点M（0，-1），当a=-2，m变化时，动点P满足
MP
=
OA
+
OB
，求动点P的纵坐标的变化范围．
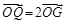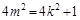
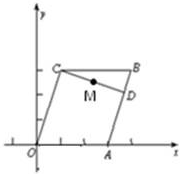
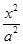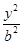已知圆C：(x－4)2＋(y－m)2＝16(m∈N*)，直线4x－3y－16＝0过椭圆E：＋＝1(a>b>0)的右焦点，且被圆C所截得的弦长为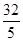，点A(3,1)在椭圆E上．
(1)求m的值及椭圆E的方程；
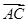(2)设Q为椭圆E上的一个动点，求·的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网