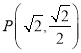题目内容
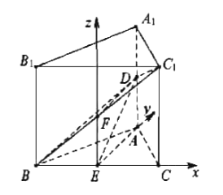
【题目】如图,在直三棱柱ABC﹣A1B1C1中,△ABC是边长为6的等边三角形,D,E分别为AA1,BC的中点.
(1)证明:AE//平面BDC1;
(2)若异面直线BC1与AC所成角的余弦值为![]() .求DE与平面BDC1所成角的正弦值.
.求DE与平面BDC1所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先证明四边形ADFE为平行四边形,则AE∥DF,由此即可得证;
(2)以点E为坐标原点,建立空间直角坐标系,设AA1=2t(t>0),根据已知条件可求得![]() ,进而求得平面BDC1的法向量以及直线DE的方向向量,再利用向量公式求解.
,进而求得平面BDC1的法向量以及直线DE的方向向量,再利用向量公式求解.
(1)证明:取BC1的中点F,连接DF,EF,
∵E为BC中点,
∴![]() ∥
∥![]() ,
,![]()
又∵D为AA1的中点,
![]() ∥
∥![]() ,
,![]() ,
,
∴![]() ∥
∥![]() ,
,![]()
![]()
∴四边形ADFE为平行四边形,
∴AE∥DF,
∵AE![]() 平面BDC1,DF
平面BDC1,DF![]() 平面BDC1,
平面BDC1,
∴AE∥平面BDC1;
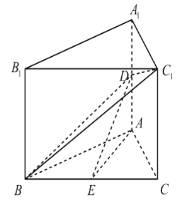
(2)由(1)及题设可知,BC,EA,EF两两互相垂直,则以点E为坐标原点,EC,EA,
EF所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
设AA1=2t(t>0),则![]() ,
,
所以![]() ,
,
故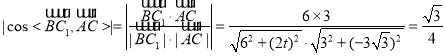
解得![]() ,
,
设平面BDC1的法向量为![]()
由 ,得
,得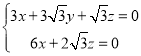 ,
,
令![]() ,则
,则![]() ,
,
又![]() ,
,
所以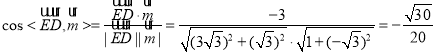 ,
,
设DE与平面BDC1所成角为![]() ,
,
则![]()
![]() ,
,
∴DE与平面BDC1所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
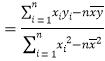 ,
,![]()