题目内容
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)若线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,且
,且![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)利用点差法可求得直线![]() 的斜率,进而求得直线
的斜率,进而求得直线![]() 的方程;
的方程;
(2)设![]() ,与椭圆方程联立得到韦达定理的形式,进而表示出
,与椭圆方程联立得到韦达定理的形式,进而表示出![]() 中点坐标;当
中点坐标;当![]() 时,易求得
时,易求得![]() 的值;当
的值;当![]() 时,可得
时,可得![]() 垂直平分线方程,进而求得
垂直平分线方程,进而求得![]() 点坐标和
点坐标和![]() ,利用弦长公式求得
,利用弦长公式求得![]() ,进而求得
,进而求得![]() 的值;综合两种情况可知
的值;综合两种情况可知![]() 为定值.
为定值.
(1)设![]() ,
,![]() ,
,
则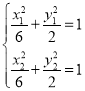 ,两式作差得:
,两式作差得:![]() ,
,
![]() 中点为
中点为![]() ,
,![]() ,
,![]() ,
,
![]() 直线
直线![]() 的方程为:
的方程为:![]() ,即:
,即:![]() .
.
(2)由椭圆方程知:![]() ,可设直线
,可设直线![]() 的方程:
的方程:![]() ,
,
联立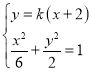 得:
得:![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,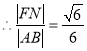 ;
;
当![]() 时,
时,![]() 的垂直平分线方程为:
的垂直平分线方程为: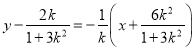 ,
,
令![]() 得:
得:![]() ,
,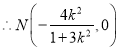 ,
,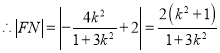 ,
,
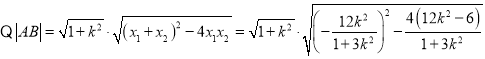
![]() ,
,
 ;
;
综上所述:![]() 为定值
为定值![]() .
.

练习册系列答案
相关题目
【题目】某区在2019年教师招聘考试中,参加![]() 、
、![]() 、
、![]() 、
、![]() 四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性应聘人数 | 男性录用人数 | 男性录用比例 | 女性应聘人数 | 女性录用人数 | 女性录用比例 |
| 269 | 167 | 62% | 40 | 24 | 60% |
| 217 | 69 | 32% | 386 | 121 | 31% |
| 44 | 26 | 59% | 38 | 22 | 58% |
| 3 | 2 | 67% | 3 | 2 | 67% |
总计 | 533 | 264 | 50% | 467 | 169 | 36% |
(1)从表中所有应聘人员中随机抽取1人,试估计此人被录用的概率;
(2)将应聘![]() 岗位的男性教师记为
岗位的男性教师记为![]() ,女性教师记为
,女性教师记为![]() ,现从应聘
,现从应聘![]() 岗位的6人中随机抽取2人.
岗位的6人中随机抽取2人.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人性别不同”,求事件
为事件“抽取的2人性别不同”,求事件![]() 发生的概率.
发生的概率.