Question

【题目】已知椭圆的长轴长为4，且经过点.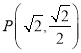

（1）求椭圆的方程；

（2）直线的斜率为，且与椭圆相交于，两点（异于点），过作的角平分线交椭圆于另一点.

（i）证明：直线与坐标轴平行；

（ii）当时，求四边形的面积

Answer 1

【答案】（1）；（2）（i）见解析，（ii）

【解析】

（1）根据题意，将点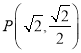代入椭圆方程即可求解.

（2）（i）利用分析法，只需证直线的方程为或，只需证，斜率都存在，且满足即可，设直线：，，，将直线与椭圆联立，消，利用韦达定理求出即可证出；（ii）可知直线和的倾斜角应该分别为，，即斜率分别为1和-1，不妨令，，求出直线的方程，将直线方程与椭圆方程联立，求出点的坐标，同理求出点，再利用三角形的面积公式即可求解.

（1）解：，将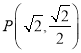代入椭圆方程，得，

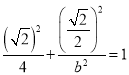解得，故椭圆的方程为.

（2）（i）证明：∵平分，欲证与坐标轴平行，

即证明直线的方程为或，

只需证，斜率都存在，且满足即可.

当或斜率不存在时，即点或点为，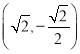

经检验，此时直线与椭圆相切，不满足题意，故，斜率都存在.

设直线：，，，

联立，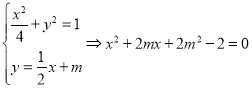

，∴，

由韦达定理得，，

，

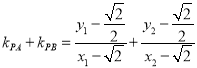
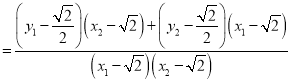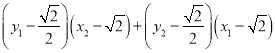
，得证.

（ii）解：若，即，

则可知直线和的倾斜角应该分别为，，

即斜率分别为1和-1，不妨就令，，

则：，即，

，

已知是其一个解，故，∴，∴，

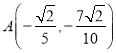同理，可得，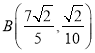

，

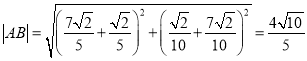因为，故的方程只能是.

设直线的倾斜角为，与所成角为，故，

而，故，∴，

又，故.