题目内容
【题目】已知函数![]() (
(![]() 为自然对数的底数),其中
为自然对数的底数),其中![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(Ⅱ)求![]() 零点的个数.
零点的个数.
【答案】(Ⅰ)函数![]() 的单调增区间是
的单调增区间是![]() ;单调减区间是
;单调减区间是![]() .(Ⅱ)当
.(Ⅱ)当![]() 或
或![]() 时,函数
时,函数![]() 只有一个零点;当
只有一个零点;当![]() 或
或![]() 时,函数
时,函数![]() 有两个零点;当
有两个零点;当![]() 时,函数
时,函数![]() 有三个零点.
有三个零点.
【解析】
(Ⅰ)对函数求导,根据导数的正负即可容易判断函数的单调性;
(Ⅱ)分离参数,构造函数![]() ,利用导数研究函数的单调性,即可容易判断.
,利用导数研究函数的单调性,即可容易判断.
(Ⅰ)当![]() 时,
时,![]() ,故可得
,故可得![]() ,
,
令![]() ,解得
,解得![]() ,
,
故![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增.
单调递增.
(Ⅱ)因为![]()
故当![]() 时,
时,![]() ,即
,即![]() 一定是函数
一定是函数![]() 的一个零点.
的一个零点.
又当![]() 时,令
时,令![]() ,分离参数可得:
,分离参数可得:
![]() ,令
,令![]() ,故可得
,故可得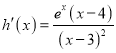 ,
,
令![]() ,解得
,解得![]() ,
,
故![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 和
和![]() 单调递减.
单调递减.
且当![]() 时,
时,![]() ,且当
,且当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,且当
,且当![]() 时,
时,![]() ;
;
又![]() ,故
,故![]() 的图像如下所示:
的图像如下所示:
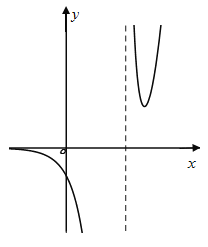
故当![]() ,即
,即![]() 时,
时,![]() 与
与![]() 有一个交点,
有一个交点,
当![]() ,即
,即![]() 时,
时,![]() 与
与![]() 有一个交点,
有一个交点,
当![]() ,即
,即![]() 时,
时,![]() 与
与![]() 有两个交点,
有两个交点,
当![]() ,即可
,即可![]() 时,
时,![]() 与
与![]() 没有交点,
没有交点,
综上所述:当![]() 时,
时,![]() 有3个零点;
有3个零点;
当![]() 时,
时,![]() 有1个零点;
有1个零点;
当![]() 或
或![]() 时,
时,![]() 有2个零点.
有2个零点.

练习册系列答案
相关题目
【题目】某小区为了了解业主用水情况,该小区分为一期和二期,入住共达4000户,现在通过随机抽样获得了100户居民的月均用水量,下图是调查结果的频数分布表和频率分布直方图.
分组 |
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 |
分组 |
|
|
|
| |
频数 | 14 | 6 | 4 | 2 |
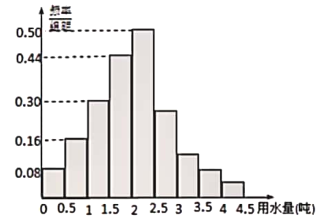
(1)估计该小区月均用水量超过3.8吨约有多少户;(2)通过频率分布直方图,估计该小区居民月均用水量平均值和中位数?