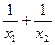题目内容
过点T（2，0）的直线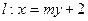
交抛物线y2=4x于A、B两点.
（I）若直线l交y轴于点M，且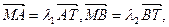
当m变化时，求
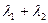的值；
（II）设A、B在直线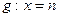
上的射影为D、E，连结AE、BD相交于一点N，则当m变化时，点N为定点的充要条件是n=－2.
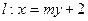交抛物线y2=4x于A、B两点.（I）若直线l交y轴于点M，且
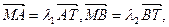当m变化时，求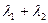的值；（II）设A、B在直线
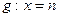上的射影为D、E，连结AE、BD相交于一点N，则当m变化时，点N为定点的充要条件是n=－2.（1）-1（2）同解析
（I）设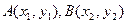
由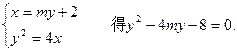
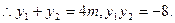
又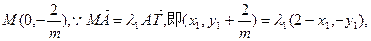
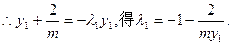
同理，由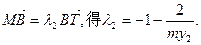
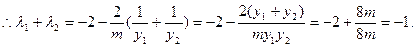
（II）方法一：当m=0时，A（2，2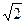
），B（2，－
），D（n，2），
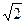E（n，－2）.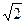
∵ABED为矩形，∴直线AE、BD的交点N的坐标为（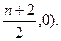
当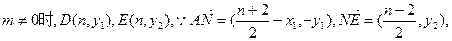
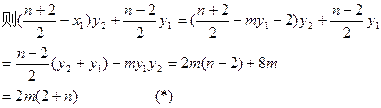
同理，对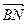
、
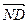进行类似计算也得（*）式
即n=－2时，N为定点（0，0）.
反之，当N为定点，则由（*）式等于0，得n=－2.
方法二：首先n=－2时，则D（－2，y1），A（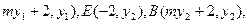
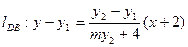①
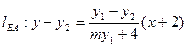②
①－②得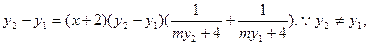
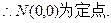
反之，若N为定点N（0，0），设此时
则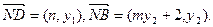
由D、N、B三点共线，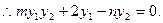
③
同理E、N、A三点共线，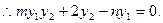
④
③+④得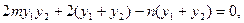
即－16m+8m－4mn=0，m(n+2)=0.
故对任意的m都有n=－2.
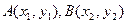
由
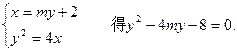
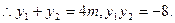
又
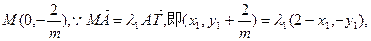
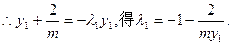
同理，由
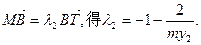
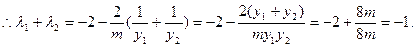
（II）方法一：当m=0时，A（2，2
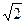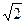），B（2，－），D（n，2），E（n，－2
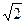）.∵ABED为矩形，∴直线AE、BD的交点N的坐标为（
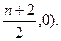
当
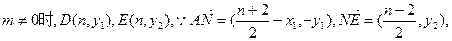
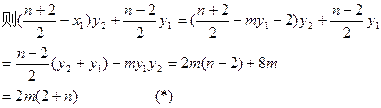
同理，对
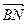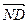、进行类似计算也得（*）式即n=－2时，N为定点（0，0）.
反之，当N为定点，则由（*）式等于0，得n=－2.
方法二：首先n=－2时，则D（－2，y1），A（
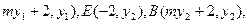
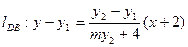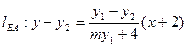① ②①－②得
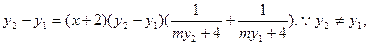
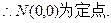
反之，若N为定点N（0，0），设此时
则
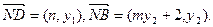
由D、N、B三点共线，
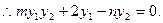③同理E、N、A三点共线，
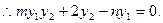④③+④得
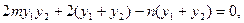
即－16m+8m－4mn=0，m(n+2)=0.
故对任意的m都有n=－2.
练习册系列答案
名校课堂系列答案
相关题目
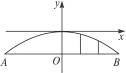
万公里时，经过地球和慧得的直线与抛物线对称轴的夹角为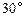
，求此慧星运行时离地球的最近距离．
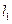过点A，且与抛物线C 相切，直线
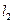:x=a(a≠-1)交抛物线C于B，交直线
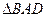的面积为S1，求
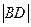及S1的值.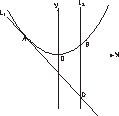
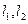所围成的图形的面积为S2，求证S1:S2的值为与a无关的常数.
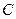经过定点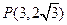
，它的一个焦点为
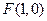，对应于该焦点的
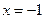，斜率为
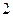的直线
交圆锥曲线
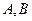两点，且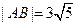
，