Question

【题目】2016年9月，第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行，在会展期间某展销商销售一种商品，根据市场调查，每件商品售价x（元）与销量t（万元）之间的函数关系如图所示，又知供货价格与销量呈反比，比例系数为20．（注：每件产品利润=售价﹣供货价格）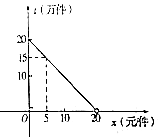
（1）求售价15元时的销量及此时的供货价格；
（2）当销售价格为多少时总利润最大，并求出最大利润．

Answer 1

【答案】
（1）解：每件商品售价x（元）与销量t（万件）之间的函数关系为t=20﹣x（0≤x≤20），

设价格为y，则y= ，x=15时，t=5万件，y=4万元

（2）解：总利润L=（x﹣ ）t=xt﹣20=x（20﹣x）﹣20≤ ﹣20=80，

当且仅当x=10元时总利润最大，最大利润80万元

【解析】（1）每件商品售价x（元）与销量t（万件）之间的函数关系为t=20﹣x（0≤x≤20），设价格为y，则y= ，即可求售价15元时的销量及此时的供货价格；（2）总利润L=（x﹣ ）t=xt﹣20=x（20﹣x）﹣20≤ ﹣20=80，可得结论．