Question

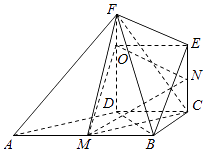
【题目】如图所示，在直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=2，AF=BF，EC∥FD，FD⊥底面ABCD，M是AB的中点．
（1）求证：平面CFM⊥平面BDF；
（2）点N在CE上，EC=2，FD=3，当CN为何值时，MN∥平面BEF．

Answer 1

【答案】
（1）证明：∵FD⊥底面ABCD，∴FD⊥AD，FD⊥BD

∵AF=BF，∴△ADF≌△BDF，∴AD=BD，

连接DM，则DM⊥AB，

∵AB∥CD，∠BCD=90°，

∴四边形BCDM是正方形，∴BD⊥CM，

∵DF⊥CM，∴CM⊥平面BDF

（2）解：（2）当CN=1，即N是CE的中点时，MN∥平面BEF．

证明如下：

过N作NO∥EF，交ED于O，连结MO，

∵EC∥FD，∴四边形EFON是平行四边形，

∵EC=2，FD=3，∴OF=1，∴OD=2，

连结OE，则OE∥DC∥MB，且OE=DC=MB，

∴四边形BMOE是平行四边形，则OM∥BE，又OM∩ON=O，

∴平面OMN∥平面BEF，

∵MN平面OMN，∴MN∥平面BEF．

【解析】（1）推导出四边形BCDM是正方形，从而BD⊥CM，又DF⊥CM，由此能证明CM⊥平面BDF．（2）过N作NO∥EF，交EF于O，连结MO，则四边形EFON是平行四边形，连结OE，则四边形BMON是平行四边形，由此能推导出N是CE的中点时，MN∥平面BEF．