题目内容
【题目】已知函数
，其中
．
（Ⅰ）当
时，求曲线
在点
处的切线方程；
（Ⅱ）求
在区间
上的最小值．（其中
是自然对数的底数）
【答案】(1) 
（2）
【解析】试题分析：（Ⅰ）求出
，可得切线斜率为
，再求出
的值，利用点斜式即可求出再
处的切线方程；（Ⅱ）对
分三种情况讨论： 
， 
， 
，分别利用导数研究函数的单调性，从而可求得函数在区间
上的最小值.
试题解析：（Ⅰ）当
时， 
， 
，
此时， 
， 
，
故曲线
在点
处的切线方程为
．
（Ⅱ）
的定义域为
令
得， 
或
当
时，
对任意的
， 
， 
在
上单调递增
② 当
时
|
|
|
|
|
| 0 |
|
| ↘ | 极小 | ↗ |
当
时，
对意的
， 
， 
在
上单调递减
由①、②、③可知，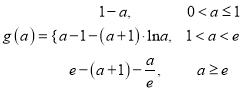 
【方法点晴】本题主要考查利用导数求曲线切线以及利用导数求函数的最值，属于难题.求曲线切线方程的一般步骤是：（1）求出
在
处的导数，即
在点
出的切线斜率（当曲线
在
处的切线与
轴平行时，在 处导数不存在，切线方程为
）；（2）由点斜式求得切线方程
.
练习册系列答案
名校课堂系列答案
相关题目
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理．
（1）若花店一天购进16枝玫瑰花，求当天的利润y（单位：元）关于当天需求量n（单位：枝，n∈N）的函数解析式．
（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率．
（i）若花店一天购进16枝玫瑰花，X表示当天的利润（单位：元），求X的分布列，数学期望及方差；
（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由．
