题目内容
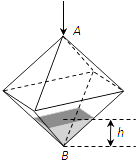
【题目】如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF,∠BFC=90°,BF=FC,H为BC的中点.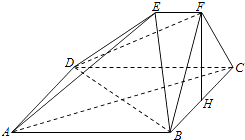
(1)求证:FH∥平面EDB;
(2)求证:AC⊥平面EDB;
(3)解:求二面角B﹣DE﹣C的大小.
【答案】
(1)证明:设AC于BD交于点G,则G为AC的中点,连接EG,GH,又H为BC的中点,
∴GH∥AB且GH= ![]() AB,又EF∥AB且EF=
AB,又EF∥AB且EF= ![]() AB,∴EF∥GH且EF=GH,
AB,∴EF∥GH且EF=GH,
∴四边形EFHG为平行四边形
∴EG∥FH,而EG平面EDB,∴FH∥平面EDB
(2)证明:由四边形ABCD为正方形,有AB⊥BC,又EF∥AB,∴EF⊥BC
而EF⊥FB,∴EF⊥平面BFC,∴EF⊥FH,∴AB⊥FH,
又BF=FC,H为BC的中点,∴FH⊥BC
∴FH⊥平面ABCD,∴FH⊥BC,FH⊥AC,
又FH∥EG,∴AC⊥EG
又AC⊥BD,EG∩BD=G,
∴AC⊥平面EDB
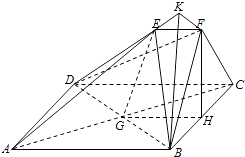
(3)EF⊥FB,∠BFC=90°,∴BF⊥平面CDEF,
在平面CDEF内过点F作FK⊥DE交DE的延长线与k,则
∠FKB为二面角B﹣DE﹣C的一个平面角,
设EF=1,则AB=2,FC= ![]() ,DE=
,DE= ![]() ,
,
又EF∥DC,∴∠KEF=∠EDC,
∴sin∠EDC=sin∠KEF= ![]() ,
,
∴FK=EFsin∠KEF= ![]() ,
,
tan∠FKB= ![]() =
= ![]() ,
,
∴∠FKB=60°,
∴二面角B﹣DE﹣C为60°.
【解析】(1)设AC于BD交于点G,则G为AC的中点,连接EG,GH,又H为BC的中点,可得四边形EFHG为平行四边形,然后利用直线与平面平行判断定理进行证明;(2)因为四边形ABCD为正方形,有AB⊥BC,又EF∥AB,可得EF⊥BC,要证FH⊥平面ABCD,FH⊥平面ABCD,从而求解.(3)在平面CDEF内过点F作FK⊥DE交DE的延长线与k,可知∠FKB为二面角B﹣DE﹣C的一个平面角,然后设EF=1,在直角三角形中进行求证.
【考点精析】关于本题考查的直线与平面平行的判定和直线与平面垂直的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.

【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下![]() 的列联表:
的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式 ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确的是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错语的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C. 有99%以上的把握认为“爱好该项运动与性别无关”
D. 有99%以上的把握认为“爱好该项运动与性别有关”
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.