题目内容
【题目】设l，m是两条不同直线，α是一个平面，则下列四个命题正确的是（ ）
A.若l⊥m，mα，则l⊥α
B.若l∥α，m∥α，则l∥m
C.若l∥α，mα，则l∥m
D.若l⊥α，l∥m，则m⊥α
【答案】D
【解析】解：A，根据线面垂直的判定定理，要垂直平面内两条相交直线才行，不正确； B：平行于同一平面的两直线可能平行，异面，相交，不正确．
C：l∥α，mα，则l∥m或两线异面，故不正确．
D：由线面垂直的性质可知：平行线中的一条垂直于这个平面则另一条也垂直这个平面．故正确．
故选D．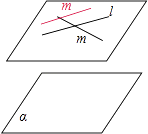
【考点精析】本题主要考查了命题的真假判断与应用和空间中直线与平面之间的位置关系的相关知识点，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系；直线在平面内—有无数个公共点；直线与平面相交—有且只有一个公共点；直线在平面平行—没有公共点才能正确解答此题．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关，通过随机抽查110名学生，得到如下
的列联表：
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式
，算得
附表：
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表，以下结论正确的是（ ）
A. 在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
B. 在犯错语的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
C. 有99%以上的把握认为“爱好该项运动与性别无关”
D. 有99%以上的把握认为“爱好该项运动与性别有关”
