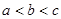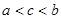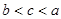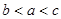��Ŀ����
�㶫ijƷ�������ҵ�IJ�Ʒ����ר��ŷ���г�����ŷծΣ����Ӱ���£�ŷ���г��������ܵ�����Ӱ�죬����ҵ�������Ĵ��������»������ع����г�������Ͷ��������Ʒ�����ƿ������������γ����г���ģ����2010��9�������ĵ�n���£�2010��9��Ϊÿһ���£�����Ʒ������������������������������������������ĺͣ��ֱ�Ϊbn��cn��an����λ���������������ͳ�����ݷ����γ�����Ӫ�����ƣ�bn��1��aan��cn��1��an��ba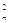 ������a��bΪ����������a1��1�����a2��1.5�����a3��1.875���.
������a��b����������a1��1�����a2��1.5�����a3��1.875���.
��1����a,b��ֵ����д��an��1��an����Ĺ�ϵʽ��
��2���������ҵ��Ʒ����������an���ֵ������ƣ��ҿ�����2������ڣ���ҵ�����������Ҳ�������ʽ�Σ������֤����an��an��1��2.
��3�������2010��9�·������ĵ�n���µ���������an����n�ı���ʽ.
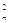 ������a��b����������a1��1�����a2��1.5�����a3��1.875���.
������a��bΪ����������a1��1�����a2��1.5�����a3��1.875���.��1����a,b��ֵ����д��an��1��an����Ĺ�ϵʽ��
��2���������ҵ��Ʒ����������an���ֵ������ƣ��ҿ�����2������ڣ���ҵ�����������Ҳ�������ʽ�Σ������֤����an��an��1��2.
��3�������2010��9�·������ĵ�n���µ���������an����n�ı���ʽ.
�⣺��1�������⣺an��1��bn��1��cn��1��aan��an��ba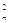 ��
��
��a2��aa1��a1��ba ����a��1��b��
����a��1��b�� ������������������
������������������
��a3��aa2��a2��ba ����
���� ����������
����������
��٢ڵ�a��1��b���� �Ӷ�an��1��2an��
�Ӷ�an��1��2an�� a
a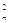 (n��N*)������������������������4�֣�
(n��N*)������������������������4�֣�
��2��֤����������an��1��2an�� a
a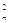 ����
���� (an��2)2��2��2.
(an��2)2��2��2.
��an��1��2��������Ƶ�a1��2��a1��1ì��.��an��1��2������an��2��
��an��1��an���� a
a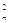 ��2an��an����
��2an��an���� an(an��2)��0��
an(an��2)��0��
����an��1��an���Ӷ�an��an��1��2.������������������������������������������9�֣�
������������ѧ���ɷ�
��������n��1ʱ��a1��1��a2��1.5����Ȼa1��a2��2������
����������n��kʱ��ak��ak��1��2����.
���ں���f(x)���� x2��2x����
x2��2x���� (x��2)2��2�ڣ�0,2����Ϊ��������
(x��2)2��2�ڣ�0,2����Ϊ��������
��f(ak)��f(ak��1)��f(2)�� ak(4��ak)��
ak(4��ak)�� ak��1(4��ak��1)��
ak��1(4��ak��1)�� ��2��(4��2)
��2��(4��2)
��ak��1��ak��2��2����.���Ͽɵ�n��N*��an��an��1��2.��������������������������9�֣�
��3����an��1��2an�� a
a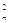 ��2(an��1��2)����(an��2)2����(2��an��1)��
��2(an��1��2)����(an��2)2����(2��an��1)�� (2��an)2��
(2��an)2��
���ɣ�2��֪an��an��1��2����֪2��an��1��0��2��an��0��
��lg(2��an��1)��2lg(2��an)��lg2����lg(2��an��1)��lg2��2��lg(2��an)��lg2��
��{lg(2��an��1)��lg2}Ϊ�ȱ����У�����Ϊ2������Ϊlg(2��a1)��lg2����lg2
��lg(2��an)��lg2��(��lg2)��2n��1����an��2�� (n��N*)Ϊ����.������������13�֣�
(n��N*)Ϊ����.������������13�֣�
 ��
����a2��aa1��a1��ba
 ����a��1��b��
����a��1��b�� ������������������
��������������������a3��aa2��a2��ba
 ����
���� ����������
������������٢ڵ�a��1��b����
 �Ӷ�an��1��2an��
�Ӷ�an��1��2an�� a
a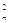 (n��N*)������������������������4�֣�
(n��N*)������������������������4�֣���2��֤����������an��1��2an��
 a
a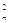 ����
���� (an��2)2��2��2.
(an��2)2��2��2.��an��1��2��������Ƶ�a1��2��a1��1ì��.��an��1��2������an��2��
��an��1��an����
 a
a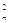 ��2an��an����
��2an��an���� an(an��2)��0��
an(an��2)��0������an��1��an���Ӷ�an��an��1��2.������������������������������������������9�֣�
������������ѧ���ɷ�
��������n��1ʱ��a1��1��a2��1.5����Ȼa1��a2��2������
����������n��kʱ��ak��ak��1��2����.
���ں���f(x)����
 x2��2x����
x2��2x���� (x��2)2��2�ڣ�0,2����Ϊ��������
(x��2)2��2�ڣ�0,2����Ϊ����������f(ak)��f(ak��1)��f(2)��
 ak(4��ak)��
ak(4��ak)�� ak��1(4��ak��1)��
ak��1(4��ak��1)�� ��2��(4��2)
��2��(4��2)��ak��1��ak��2��2����.���Ͽɵ�n��N*��an��an��1��2.��������������������������9�֣�
��3����an��1��2an��
 a
a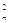 ��2(an��1��2)����(an��2)2����(2��an��1)��
��2(an��1��2)����(an��2)2����(2��an��1)�� (2��an)2��
(2��an)2�����ɣ�2��֪an��an��1��2����֪2��an��1��0��2��an��0��
��lg(2��an��1)��2lg(2��an)��lg2����lg(2��an��1)��lg2��2��lg(2��an)��lg2��
��{lg(2��an��1)��lg2}Ϊ�ȱ����У�����Ϊ2������Ϊlg(2��a1)��lg2����lg2
��lg(2��an)��lg2��(��lg2)��2n��1����an��2��
 (n��N*)Ϊ����.������������13�֣�
(n��N*)Ϊ����.������������13�֣���

��ϰ��ϵ�д�
�����Ŀ
 ������
������
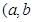 Ϊ�������ϵ�ֵ����
Ϊ�������ϵ�ֵ���� ������������������
������������������ ���� �� �ԣ�
���� �� �ԣ� �Ƕ�����ʵ����R�ϵ��溯������
�Ƕ�����ʵ����R�ϵ��溯������ ��0ʱ��
��0ʱ��
 ����
����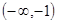 ���ǵ�������������a��ȡֵ��Χ��
���ǵ�������������a��ȡֵ��Χ��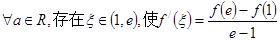 .
.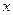 �ķ���
�ķ���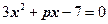 �Ľ⼯Ϊ
�Ľ⼯Ϊ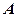 ������
������ �Ľ⼯Ϊ
�Ľ⼯Ϊ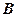 ����
����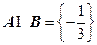 ����
����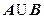
 ���㣺
���㣺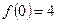 ��
�� ���Ҹú�������СֵΪ1.
���Ҹú�������СֵΪ1.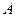 =
=  .(����
.(����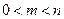 ). ���Ƿ��������������ʵ��
). ���Ƿ��������������ʵ�� ,ʹ�ú���
,ʹ�ú���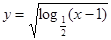 �Ķ�����Ϊ
�Ķ�����Ϊ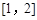
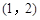

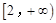
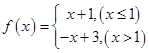 ����ô
����ô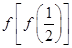 ��ֵ�ǣ� ��
��ֵ�ǣ� ��
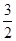
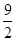
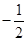
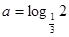 ��
��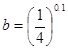 ��
��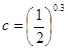 ����( )
����( )