题目内容
16.已知关于实数x,y的方程组$\left\{\begin{array}{l}{{x}^{3}+{y}^{3}=2}\\{y=kx+d}\end{array}\right.$没有实数解,则实数k,d的取值范围为k=-1,d≤0或d>2.分析 法一:消去y后,化简方程,利用方程的解的情况,讨论求解即可.
法二:转化方程组的两个方程为函数图象的交点问题,作出函数的图象,求解即可.
解答 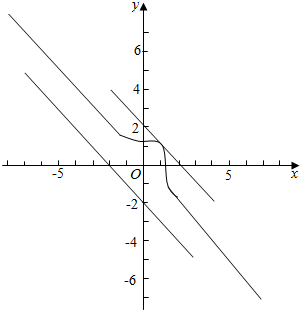 解:法一:将y=kx+d代入x3+y3=2得:
解:法一:将y=kx+d代入x3+y3=2得:
x3+(kx+d)3-2=0 无解,
展开得:
(1+k3)x3+3k2dx2+3kd2x+d3-2=0,
若k≠-1,则这是三次方程,至少有一个实根,不符题意;
若k=-1,方程化为:3dx2-3d2x+d3-2=0,
若d=0,则方程化为-2=0,矛盾;满足题意.
若d≠0,这是二次方程,无解则判别式<0,得:(3d2)2-4*3d(d3-2)<0,即:d(-d3+8)<0,得d>2或d<0.
综合得:k=-1,d<0或d>2.
法二关于实数x,y的方程组$\left\{\begin{array}{l}{{x}^{3}+{y}^{3}=2}\\{y=kx+d}\end{array}\right.$没有实数解,
也就是$\left\{\begin{array}{l}y=\root{3}{{2-x}^{3}}\\ y=kx+d\end{array}\right.$没有实数解,
在平面直角坐标系中,画出两个函数的图象如图:
可知:两个函数没有交点,k=-1,d≤0或d>2.
故答案为:k=-1,d≤0或d>2.
点评 本题考查函数的图象的作法,考查转化思想以及计算能力,是难度比较大的题目.

练习册系列答案
相关题目