题目内容
11.已知在数列{an}中,a1=1,an+1=3an+1,求数列{an}的通项公式.分析 把递推关系式化简得出an+1$+\frac{1}{2}$=3(an$+\frac{1}{2}$),即$\frac{{a}_{n+1}+\frac{1}{2}}{{a}_{n}+\frac{1}{2}}$=3=常数.构造等比数列,运用等比数列求解an$+\frac{1}{2}$=$\frac{3}{2}$×3n-2=$\frac{1}{2}×{3}^{n}$,即可得出an.
解答 解:∵an+1=3an+1,
∴an+1$+\frac{1}{2}$=3(an$+\frac{1}{2}$),
即$\frac{{a}_{n+1}+\frac{1}{2}}{{a}_{n}+\frac{1}{2}}$=3=常数.
∴数列{an$+\frac{1}{2}$}是等比数列,首项为1$+\frac{1}{2}$=$\frac{3}{2}$,公比为3,
∴an$+\frac{1}{2}$=$\frac{3}{2}$×3n-2=$\frac{1}{2}×{3}^{n}$,
故数列{an}的通项公式an=$\frac{1}{2}×{3}^{n}$$-\frac{1}{2}$
点评 本题考查了等比数列的通项公式,考查了变形能力,考查了推理能力与计算能力,属于中档题

练习册系列答案
相关题目
1.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AC=12,BC=5,则CD的长为( )
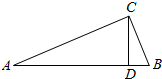

| A. | $\frac{60}{13}$ | B. | $\frac{120}{13}$ | C. | $\frac{50}{13}$ | D. | $\frac{70}{13}$ |
2.已知α,β都是锐角,cosα=$\frac{3}{5}$,cos(α+β)=-$\frac{\sqrt{2}}{2}$,则cosβ的值为( )
| A. | -$\frac{7\sqrt{2}}{10}$ | B. | $\frac{\sqrt{2}}{10}$ | C. | $\frac{\sqrt{2}}{5}$ | D. | $\frac{7\sqrt{2}}{5}$ |
20.某校高一.2班学生每周用于数学学习的时间x(单位:h)与数学成绩y(单位:分)之间有如下数据:
某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |