题目内容
5．设x1、x2是关于x的二次方程x2-2kx+1-k2=0的两个实根，k为实数，则$x_1^2+x_2^2$的最小值为（ ）| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
分析 x1，x2是方程x2-2kx+1-k2=0的两个实数根，故方程有实数根，则△≥0，由此不难求出参数K的范围，而要求x12+x22的最小值可以先将x12+x22化为（x1+x2）2-2x1•x2的形式再利用韦达定理（即一元二次方程根与系数的关系）将其转化为关于K的不等式，进面求出x12+x22的最小值．
解答 解：∵x1，x2是方程x2-2kx+1-k2=0的两个实数根．
△=（2k）2-4（1-k2）=8k2-4≥0．
即k2≥$\frac{1}{2}$．
又∵x1+x2=2k，x1•x2=1-k2．
∴x12+x22=（x1+x2）2-2x1•x2=6k2-2≥1．
故x12+x22的最小值为1．
故选：C．
点评 代数的核心内容是函数，但由于函数、不等式、方程之间的辩证关系，故我们在解决函数问题是经常要用到方程的性质，其中韦达定理是最重要的方程的性质，需要好好学习．
练习册系列答案
相关题目
20．某校高一.2班学生每周用于数学学习的时间x（单位：h）与数学成绩y（单位：分）之间有如下数据：
某同学每周用于数学学习的时间为18小时，试预测该生数学成绩．
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
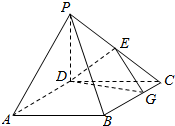如图，四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD为正方形，BC=PD=2，E为PC的中点，G在BC上，且CG=$\frac{1}{3}$CB
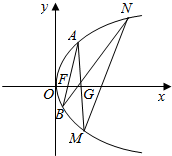如图，已知抛物线C：y2=2px（p＞0），焦点为F，过点G（p，0）作直线l交抛物线C于A，M两点，设A（x1，y1），M（x2，y2）．