题目内容
1.设$\overrightarrow{a}$,$\overrightarrow{b}$是两个不共线的向量,已知$\overrightarrow{AB}$=2$\overrightarrow{a}$+m$\overrightarrow{b}$,$\overrightarrow{CB}$=$\overrightarrow{a}$+3$\overrightarrow{b}$,若A、B、C三点共线,则m的值为:6.分析 根据条件向量$\overrightarrow{AB}$与$\overrightarrow{CB}$共线,从而存在k使得,$\overrightarrow{AB}=k\overrightarrow{CB}$,从而便得到2$\overrightarrow{a}$$+m\overrightarrow{b}$=$k\overrightarrow{a}+3k\overrightarrow{b}$,从而便得到$\left\{\begin{array}{l}{2=k}\\{m=3k}\end{array}\right.$,这样即可解出m.
解答 解:A,B,C三点共线;
∴向量$\overrightarrow{AB}$,$\overrightarrow{CB}$共线;
∴存在实数k,使$\overrightarrow{AB}=k\overrightarrow{CB}$;
∴$2\overrightarrow{a}+m\overrightarrow{b}=k\overrightarrow{a}+3k\overrightarrow{b}$;
$\overrightarrow{a}$与$\overrightarrow{b}$不共线;
∴$\left\{\begin{array}{l}{2=k}\\{m=3k}\end{array}\right.$;
∴m=6.
故答案为:6.
点评 考查共线向量基本定理,向量的数乘运算,以及平面向量基本定理.

练习册系列答案
相关题目
12.根据给出的数塔猜测123456×9+2等于( )
1×9+2=11
12×9+2=111
123×9+2=1111
1234×9+2=11111
12345×9+2=111111.
1×9+2=11
12×9+2=111
123×9+2=1111
1234×9+2=11111
12345×9+2=111111.
| A. | 111111 | B. | 1111111 | C. | 1111112 | D. | 1111110 |
11.函数 f(x)=(x-2014)(x+2015)的图象与x轴,y轴有三个交点,有一个圆恰经过这三个点,则此圆与坐标轴的另一个交点是( )
| A. | (0,-1) | B. | (0,1) | C. | (0,$\sqrt{2014×2015}$) | D. | (0,$\sqrt{\frac{2014}{2015}}$) |
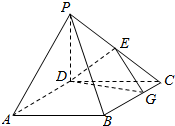 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,G在BC上,且CG=$\frac{1}{3}$CB
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,G在BC上,且CG=$\frac{1}{3}$CB