题目内容
6.在当今社会,随科技的进步,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量y(单位:千套)与销售价格x(单位:元/套)满足的关系式y=$\frac{a}{x-2}$+4(x-6)2,其中2<x<6,a为常数.已知销售价格为4元/套时,每日可售出套题21千套.(Ⅰ)求a的值;
(Ⅱ)假设网校的员工工资、办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格x的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
分析 (Ⅰ)由题意可得$\frac{a}{2}$+16=21,从而解得;
(Ⅱ)由(Ⅰ)知套题每日的销售量y=$\frac{10}{x-2}$+4(x-6)2,从而可得每日销售套题所获得的利润f(x)=(x-2)[$\frac{10}{x-2}$+4(x-6)2]=4x3-56x2+240x-278(2<x<6);求导f′(x)=4(3x-10)(x-6),从而确定函数的单调性与最值即可.
解答 解:(Ⅰ)∵x=4时,y=21,
∴$\frac{a}{2}$+16=21,
解得,a=10;
(Ⅱ)由(Ⅰ)知,
套题每日的销售量y=$\frac{10}{x-2}$+4(x-6)2,
所以每日销售套题所获得的利润
f(x)=(x-2)[$\frac{10}{x-2}$+4(x-6)2]
=10+4(x-6)2(x-2)
=4x3-56x2+240x-278(2<x<6);
则f′(x)=4(3x-10)(x-6),
故f(x)在(2,$\frac{10}{3}$)上单调递增,在($\frac{10}{3}$,6)上单调递减;
∴x=$\frac{10}{3}$是函数f(x)在(2,6)内的极大值点,也是最大值点;
∴当x≈3.3时,函数f(x)取得最大值.
点评 本题考查了函数在实际问题中的应用及导数的综合应用,属于中档题.

练习册系列答案
相关题目
11.函数 f(x)=(x-2014)(x+2015)的图象与x轴,y轴有三个交点,有一个圆恰经过这三个点,则此圆与坐标轴的另一个交点是( )
| A. | (0,-1) | B. | (0,1) | C. | (0,$\sqrt{2014×2015}$) | D. | (0,$\sqrt{\frac{2014}{2015}}$) |
18.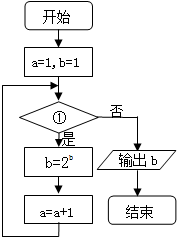 已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )
已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )
 已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )
已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )| A. | a>3? | B. | a≥3? | C. | a≤3? | D. | a<3? |
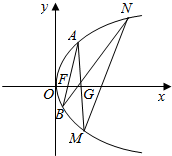 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).