题目内容
8.已知函数f(x)=Asin(ωx+φ)(A,ω>0,|φ|<$\frac{π}{2}$)的图象在y轴右侧的第一个最高点为P($\frac{1}{3}$,2),在y轴右侧与x轴的第一个交点为R($\frac{5}{6}$,0).(1)求函数y的解析式;
(2)已知方程f(x)-m=0在区间[-$\frac{1}{2},\frac{2}{3}}$]上有解,求实数m的取值范围.
分析 (1)由题意可得A,$\frac{T}{4}=\frac{5}{6}-\frac{1}{3}=\frac{1}{2}$,由周期公式可求ω,将点P($\frac{1}{3}$,2)代入解析式,解得φ,从而可求函数y的解析式.
(2)由$x∈[{-\frac{1}{2},\frac{2}{3}}]$,可求得$({πx+\frac{π}{6}})∈[{-\frac{π}{3},\frac{5π}{6}}]$,从而可求$f(x)∈[{-\sqrt{3},2}]$,方程f(x)-m=0即m=f(x)在[-$\frac{1}{2},\frac{2}{3}}$]有解,由正弦函数的图象和性质即可得解.
解答 (本题12分)
解:(1)由题意,A=2,$\frac{T}{4}=\frac{5}{6}-\frac{1}{3}=\frac{1}{2}$,所以T=2,
故$\frac{2π}{ω}=2$,解得ω=π,所以f(x)=2sin(πx+φ),
将点P($\frac{1}{3}$,2),代入上式,解得$φ=\frac{π}{6}$,
所以,$f(x)=2sin({πx+\frac{π}{6}})$.
(2)因为$x∈[{-\frac{1}{2},\frac{2}{3}}]$,所以$({πx+\frac{π}{6}})∈[{-\frac{π}{3},\frac{5π}{6}}]$,
此时,$sin({πx+\frac{π}{6}})∈[{-\frac{{\sqrt{3}}}{2},1}]$,故$f(x)∈[{-\sqrt{3},2}]$,
方程f(x)-m=0即m=f(x)在[-$\frac{1}{2},\frac{2}{3}}$]有解,所以$m∈[{-\sqrt{3},2}]$.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质,属于基本知识的考查.

 习题精选系列答案
习题精选系列答案| A. | 20 | B. | 19 | C. | 10 | D. | 9 |
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
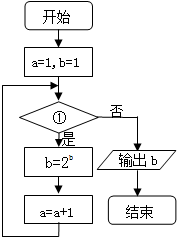 已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )
已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )| A. | a>3? | B. | a≥3? | C. | a≤3? | D. | a<3? |