题目内容
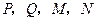 四点都在椭圆
四点都在椭圆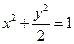 上,
上,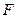 为椭圆在
为椭圆在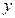 轴正半轴上的焦点.已知
轴正半轴上的焦点.已知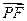 与
与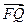 共线,
共线,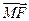 与
与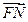 共线,且
共线,且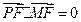 .求四边形
.求四边形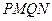 的面积的最小值和最大值.
的面积的最小值和最大值.四边形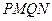 面积的最大值为
面积的最大值为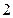 ,最小值为
,最小值为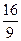
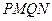 面积的最大值为
面积的最大值为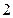 ,最小值为
,最小值为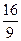
由条件知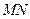 和
和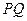 是椭圆的两条弦,相交于焦点
是椭圆的两条弦,相交于焦点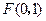 ,且
,且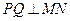 ,直线
,直线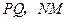 中至少有一条存在斜率,不妨设
中至少有一条存在斜率,不妨设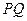 的斜率为
的斜率为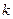 .又
.又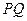 过点
过点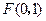 ,故
,故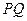 方程为
方程为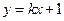 .将此式代入椭圆方程得
.将此式代入椭圆方程得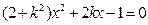 .
.
设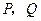 两点的坐标分别为
两点的坐标分别为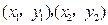 ,
,
则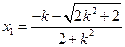 ,
,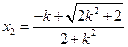 .
.
从而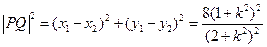 ,
,
亦即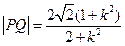 .
.
(Ⅰ)当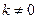 时,
时,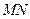 的斜率为
的斜率为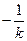 ,同上可推得
,同上可推得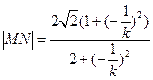 .
.
故四边形面积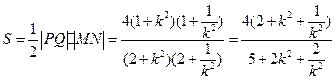 .
.
令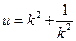 ,得
,得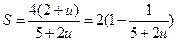 .
.
因为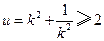 ,当
,当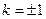 时,
时,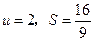 ,且
,且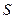 是以
是以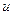 为自变量的增函数,所以
为自变量的增函数,所以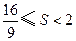 .
.
(Ⅱ)当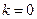 时,
时,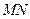 为椭圆的长轴,
为椭圆的长轴,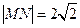 ,
,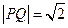 ,
,
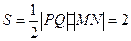 .
.
综合(Ⅰ),(Ⅱ)知,四边形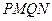 面积的最大值为
面积的最大值为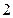 ,最小值为
,最小值为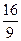 .
.
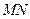 和
和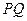 是椭圆的两条弦,相交于焦点
是椭圆的两条弦,相交于焦点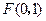 ,且
,且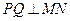 ,直线
,直线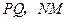 中至少有一条存在斜率,不妨设
中至少有一条存在斜率,不妨设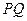 的斜率为
的斜率为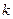 .又
.又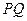 过点
过点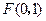 ,故
,故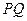 方程为
方程为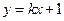 .将此式代入椭圆方程得
.将此式代入椭圆方程得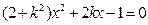 .
.设
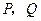 两点的坐标分别为
两点的坐标分别为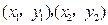 ,
,则
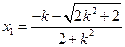 ,
,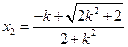 .
.从而
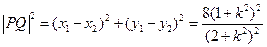 ,
,亦即
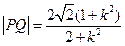 .
.(Ⅰ)当
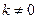 时,
时,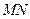 的斜率为
的斜率为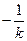 ,同上可推得
,同上可推得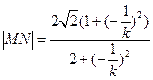 .
.故四边形面积
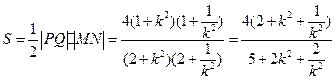 .
.令
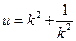 ,得
,得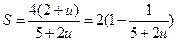 .
.因为
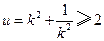 ,当
,当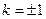 时,
时,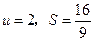 ,且
,且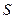 是以
是以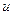 为自变量的增函数,所以
为自变量的增函数,所以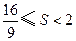 .
.(Ⅱ)当
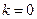 时,
时,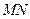 为椭圆的长轴,
为椭圆的长轴,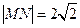 ,
,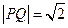 ,
,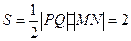 .
.综合(Ⅰ),(Ⅱ)知,四边形
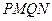 面积的最大值为
面积的最大值为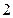 ,最小值为
,最小值为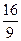 .
.
练习册系列答案
相关题目
 上的动点
上的动点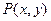 及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是
及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是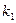 ,
,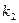 ,且
,且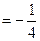 。(1)求动点P的轨迹C的方程;
。(1)求动点P的轨迹C的方程;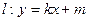 与曲线C交于M,N两点,且直线BM,BN的斜率都存在并满足
与曲线C交于M,N两点,且直线BM,BN的斜率都存在并满足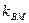 ·
·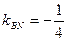 ,求证:直线
,求证:直线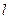 过原点。
过原点。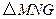 中,已知
中,已知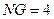 .当动点
.当动点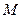 满足条件
满足条件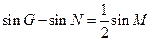 时,求动点
时,求动点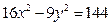 的左、右两个焦点分别为
的左、右两个焦点分别为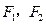 ,点
,点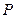 在双曲线上,且
在双曲线上,且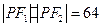 ,求
,求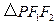 的面积.
的面积.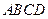 中,
中,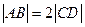 ,点
,点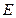 分有向线段
分有向线段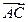 所成的比为
所成的比为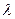 ,双曲线过
,双曲线过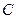 ,
,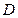 ,
,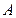 ,
,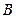 为焦点,当
为焦点,当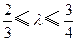 时,求双曲线离心率
时,求双曲线离心率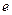 的取值范围.
的取值范围.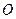 ,焦点在
,焦点在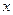 轴上,斜率为
轴上,斜率为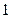 且过椭圆右焦点
且过椭圆右焦点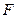 的直线交椭圆于
的直线交椭圆于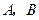 两点,
两点,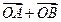 与
与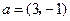 共线.设
共线.设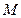 为椭圆上任意一点,且
为椭圆上任意一点,且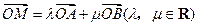 ,证明
,证明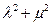 为定值.
为定值.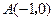 ,
, ,动点
,动点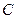 满足
满足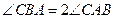 ,求动点
,求动点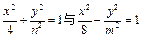 有相同的准线,则动点P (n, m)的轨迹为
有相同的准线,则动点P (n, m)的轨迹为