题目内容
已知:函数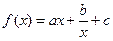 (
(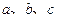 是常数)是奇函数,且满足
是常数)是奇函数,且满足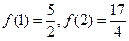 ,
,
(Ⅰ)求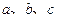 的值;
的值;
(Ⅱ)试判断函数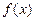 在区间
在区间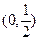 上的单调性并说明理由;
上的单调性并说明理由;
(Ⅲ)试求函数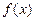 在区间
在区间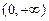 上的最小值.
上的最小值.
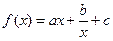 (
(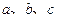 是常数)是奇函数,且满足
是常数)是奇函数,且满足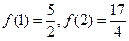 ,
,(Ⅰ)求
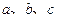 的值;
的值;(Ⅱ)试判断函数
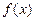 在区间
在区间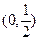 上的单调性并说明理由;
上的单调性并说明理由;(Ⅲ)试求函数
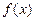 在区间
在区间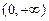 上的最小值.
上的最小值.
(Ⅰ)
 ,
, .
. (Ⅱ)函数
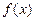 在区间
在区间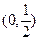 上为减函数.
上为减函数. (Ⅲ)
 是函数的最小值点,即函数
是函数的最小值点,即函数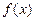 在
在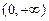 取得最小值
取得最小值 .
. (Ⅰ)∵函数
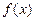 是奇函数,则
是奇函数,则
即
 ∴
∴ …………………………2分
…………………………2分由
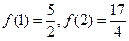 得
得 解得
解得
∴
 ,
, . …………………………5分
. …………………………5分(Ⅱ)由(Ⅰ)知
 , ∴
, ∴ , ………………6分
, ………………6分当
 时
时 ,
, …………………………8分
…………………………8分∴
 ,即函数
,即函数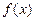 在区间
在区间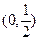 上为减函数. …………………………9分
上为减函数. …………………………9分(Ⅲ)由
 =0,
=0, 得
得 …………………………11分
…………………………11分∵当
 ,
, ,∴
,∴ ,
, 即函数
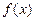 在区间
在区间 上为增函数 …………………………13分
上为增函数 …………………………13分∴
 是函数的最小值点,即函数
是函数的最小值点,即函数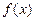 在
在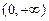 取得最小值
取得最小值 . ………14分
. ………14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
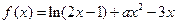 在
在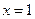 处取得极值.
处取得极值.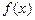 的单调区间;
的单调区间;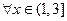 ,
,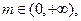
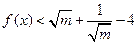 .
.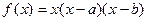 ,点A(s,f(s)), B(t,f(t))
,点A(s,f(s)), B(t,f(t))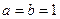 ,求函数
,求函数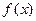 的单调递增区间;
的单调递增区间; 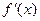 满足:当|x|≤1时,有|
满足:当|x|≤1时,有|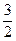 恒成立,求函数
恒成立,求函数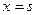 和
和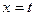 处取得极值,且
处取得极值,且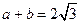 ,证明:
,证明: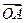 与
与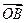 不可能垂直.
不可能垂直.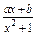 ,b为常数.
,b为常数.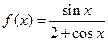 。
。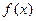 的单调区间;
的单调区间;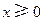 ,都有
,都有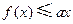 ,求
,求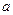 的取值范围。
的取值范围。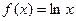 ,
,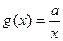 ,设
,设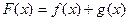 .
.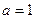 时,求函数
时,求函数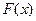 的单调区间;
的单调区间;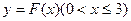 图象上任意一点
图象上任意一点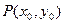 为切点的切线斜率
为切点的切线斜率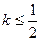 恒成立,求实数
恒成立,求实数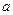 的最小值.
的最小值. 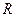 上的奇函数
上的奇函数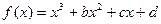 在
在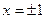 处取得极值.
处取得极值.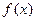 的解析式;
的解析式;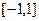 上任意两个自变量的值
上任意两个自变量的值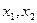 ,都有
,都有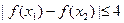 成立;
成立;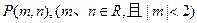 可作曲线
可作曲线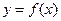 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.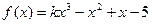 在R上单调递增,记
在R上单调递增,记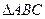 的三内角
的三内角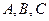 的对应边分别为
的对应边分别为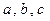 ,若
,若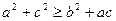 时,不等式
时,不等式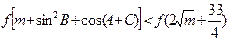 恒成立.
恒成立.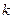 的取值范围;
的取值范围;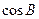 的取值范围;
的取值范围;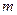 的取值范围.
的取值范围.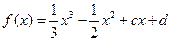 有极值.
有极值.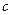 的取值范围;
的取值范围;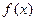 在
在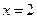 处取得极值,且当
处取得极值,且当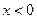 时,
时,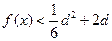 恒成立,求
恒成立,求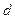 的取值范围.
的取值范围.