题目内容
【题目】在平面直角坐标系中,![]() 的顶点
的顶点![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
(1)求![]() 的顶点
的顶点![]() 的轨迹方程;
的轨迹方程;
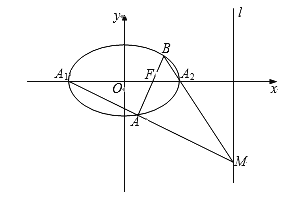
(2)直线![]() 与顶点
与顶点![]() 的轨迹交于
的轨迹交于![]() 两点,当线段
两点,当线段![]() 的中点
的中点![]() 落在直线
落在直线![]() 上时,试问:线段
上时,试问:线段![]() 的垂直平分线是否恒过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
的垂直平分线是否恒过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
【答案】(1)![]() (2)恒过定点;定点
(2)恒过定点;定点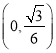
【解析】
(1)由正弦定理,结合椭圆定义,即可容易求得轨迹方程;
(2)联立直线方程和椭圆方程,由韦达定理求得中点![]() 的坐标,根据其纵坐标为
的坐标,根据其纵坐标为![]() ,即可求得
,即可求得![]() 的等量关系,再求出直线
的等量关系,再求出直线![]() 垂直平分线的方程,再求直线恒过的定点即可.
垂直平分线的方程,再求直线恒过的定点即可.
(1)在![]() 中,
中,![]() ,
,
根据正弦定理,可得![]() ,且
,且![]() ,
,
由椭圆定义,可知顶点![]() 的轨迹为中心在原点,
的轨迹为中心在原点,
以![]() 为焦点的椭圆(不包括与
为焦点的椭圆(不包括与![]() 轴交点).
轴交点).
![]() ,
,![]() ,
,![]() ,
,
![]() 轨迹方程为
轨迹方程为![]() .
.
(2)设![]() ,
,![]() ,
,
由 ,得
,得![]() ,
,
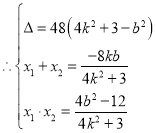 ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() 落在直线
落在直线![]() 上,
上,
![]() ,
,![]() ,
,
![]() ,
,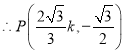 ,
,
![]() 线段
线段![]() 的垂直平分线方程为
的垂直平分线方程为 ,即
,即![]() ,
,
![]() 线段
线段![]() 的垂直平分线恒过定点
的垂直平分线恒过定点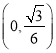 .
.

练习册系列答案
相关题目