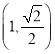题目内容
【题目】设函数![]()
![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 的极大值点为
的极大值点为![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)答案见解析;(Ⅱ)证明见解析.
【解析】分析:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]() ,据此分类讨论可得:当
,据此分类讨论可得:当![]() 时,函数
时,函数![]() 在区间
在区间![]() 单调递增;当
单调递增;当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(Ⅱ)由(Ⅰ)知![]() ,原问题等价于证明
,原问题等价于证明![]() .构造函数
.构造函数![]()
![]() ,结合导函数的特征再次构造函数
,结合导函数的特征再次构造函数![]() ,结合函数的性质即可证得题中的结论.
,结合函数的性质即可证得题中的结论.
详解:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则函数
,则函数![]() 在区间
在区间![]() 单调递增;
单调递增;
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() .
.
所以,![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
所以,函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 单调递减.
单调递减.
综上所述,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 单调递增;
单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(Ⅱ)由(Ⅰ)知![]() 且
且![]() 时,解得
时,解得![]() .
.![]() ,
,
要证![]() ,即证
,即证![]() ,即证:
,即证:![]() .
.
令![]()
![]() ,则
,则![]()
![]() .
.
令![]() ,易见函数
,易见函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
而![]() ,
,![]() ,
,
所以在区间![]() 上存在唯一的实数
上存在唯一的实数![]() ,使得
,使得![]() ,
,
即![]() ,且
,且![]() 时
时![]() ,
,![]() 时
时![]() .
.
故![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
∴![]()
![]() .
.
又![]() ,∴
,∴![]()
![]() .
.
∴![]() 成立,即
成立,即![]() 成立.
成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目