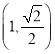题目内容
【题目】在无穷数列![]() 中,
中,![]() ,且
,且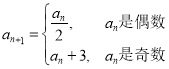 ,记
,记![]() 的前n项和为
的前n项和为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)证明:![]() 中必有一项为1或3.
中必有一项为1或3.
【答案】(1)37(2)5(3)证明见解析
【解析】
(1)计算数列前9项,再计算和得到答案.
(2)讨论![]() 为偶数,
为偶数,![]() 为偶数,
为偶数,![]() 为偶数,
为偶数,![]() 为奇数,
为奇数,![]() 为奇数,
为奇数,![]() 为偶数,
为偶数,![]() 为奇数,
为奇数,![]() 为奇数四种情况,计算得到答案.
为奇数四种情况,计算得到答案.
(2)设![]() 中最小的奇数为
中最小的奇数为![]() ,则
,则![]() ,
,![]() ,讨论
,讨论![]() 为奇数,
为奇数,![]() 为偶数两种情况,计算得到答案.
为偶数两种情况,计算得到答案.
(1)![]() ,故
,故![]() ,故
,故![]() .
.
(2)当![]() 为偶数,
为偶数,![]() 为偶数时,
为偶数时,![]() ,无整数解;
,无整数解;
当![]() 为偶数,
为偶数,![]() 为奇数时,
为奇数时,![]() ,解得
,解得![]() ,验证不成立;
,验证不成立;
当![]() 为奇数,
为奇数,![]() 为偶数时,
为偶数时,![]() ,解得
,解得![]() ,验证成立;
,验证成立;
当![]() 为奇数,
为奇数,![]() 为奇数时,
为奇数时,![]() ,无整数解;
,无整数解;
综上所述:![]() .
.
(3)设![]() 中最小的奇数为
中最小的奇数为![]() ,则
,则![]() ,
,![]() ,
,
若![]() 为奇数,则
为奇数,则![]() ,解得
,解得![]() ;
;
若![]() 为偶数,则
为偶数,则![]() ,
,![]() ,
,![]() 为奇数,解得
为奇数,解得![]() ;
;
又![]() ,∴
,∴![]() 中必有一项为1或3.
中必有一项为1或3.
综上所述:![]() ,故
,故![]() 中必有一项为1或3.
中必有一项为1或3.

练习册系列答案
相关题目