题目内容
已知函数f(x)=x3-x2+bx+a(a,b∈R),且其导函数f′(x)的图象过原点.
(1)若存在x<0,使得f′(x)=-9,求a的最大值;
(2)当a>0时,求函数f(x)的极值.
(1)若存在x<0,使得f′(x)=-9,求a的最大值;
(2)当a>0时,求函数f(x)的极值.
f(x)=x3-x2+bx+a,f′(x)=x2-(a+1)x+b
由f′(0)=0得b=0,f′(x)
=x(x-a-1).
(1)存在x<0,使得f′(x)
=x(x-a-1)=-9,
-a-1=-x-=(-x)+≥2=6,
∴a≤-7,
当且仅当x=-3时,a=-7.所以a的最大值为-7.
(2)当a>0时,x,f′(x),f(x)的变化情况如下表:
f(x)的极大值f(0)=a>0,
f(x)的极小值f(a+1)
=a-(a+1)3
由f′(0)=0得b=0,f′(x)
=x(x-a-1).
(1)存在x<0,使得f′(x)
=x(x-a-1)=-9,
-a-1=-x-=(-x)+≥2=6,
∴a≤-7,
当且仅当x=-3时,a=-7.所以a的最大值为-7.
(2)当a>0时,x,f′(x),f(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0, a+1) | a+1 | (a+1, +∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) |  ? ? | 极大值 |  ? ? | 极小值 |  ? ? |
f(x)的极小值f(a+1)
=a-(a+1)3
略

练习册系列答案
相关题目
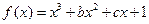 的单调减区间是(1,2)
的单调减区间是(1,2)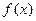 的解析式;
的解析式;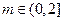 ,关于
,关于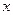 的不等式
的不等式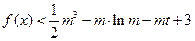 在
在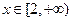 时有解,求实数
时有解,求实数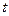 的取值范围.
的取值范围.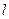 过点
过点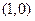 ,且与曲线
,且与曲线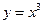 和
和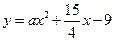 都相切,
都相切,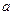 的值。
的值。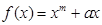 的导函数为
的导函数为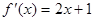 ,则数列
,则数列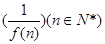 的前
的前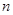 项
项
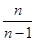


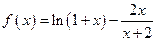 ,证明:当
,证明:当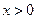 时,
时,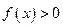
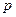 ,证明:
,证明: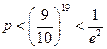
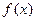 =
=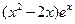 (e为自然对数的底数)
(e为自然对数的底数) 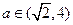 ,求函数
,求函数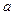 ]上的最大值和最小值.(5分)
]上的最大值和最小值.(5分)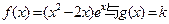 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围.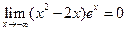 )(2分)
)(2分)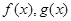 都是定义在R上的函数,且
都是定义在R上的函数,且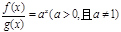 ,
,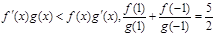 ,则
,则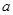 的值为( )
的值为( )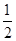
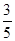
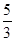
 ,
,
 ,n∈N,
,n∈N, ( )
( ) 
