题目内容
如右图所示,已知A为抛物线C:y=2x2上的点,直线l1过点A,且
与抛物线C相切,直线l2:x=a交抛物线C于点B,交直线l1于点D.
(1)求直线l1的方程;
(2)求△ABD的面积S1.
与抛物线C相切,直线l2:x=a交抛物线C于点B,交直线l1于点D.
(1)求直线l1的方程;
(2)求△ABD的面积S1.
(1)由条件知点A为直线l1与抛物线C的切点,
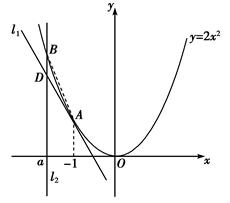
∵y′=4x,∴直线l1的斜率k=-4,
即直线l1的方程为y-2=-4(x+1), 即4x+y+2=0.
(2)点A的坐标为(-1,2),
由条件可求得点B的坐标为(a,2a2),
点D的坐标为(a,-4a-2),∴△ABD的面积S1为
S1=×|2a2-(-4a-2)|×|-1-a|
=|(a+1)3|=-(a+1)3.

∵y′=4x,∴直线l1的斜率k=-4,
即直线l1的方程为y-2=-4(x+1), 即4x+y+2=0.
(2)点A的坐标为(-1,2),
由条件可求得点B的坐标为(a,2a2),
点D的坐标为(a,-4a-2),∴△ABD的面积S1为
S1=×|2a2-(-4a-2)|×|-1-a|
=|(a+1)3|=-(a+1)3.
略

练习册系列答案
相关题目
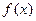 =
=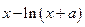 在
在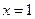 处取得极值.
处取得极值.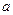 的值;
的值;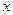 的方程
的方程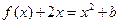 在
在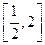 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数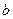 的取值范围;
的取值范围;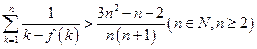 .参考数据:
.参考数据: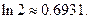
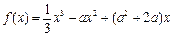 ,
,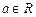 .
.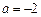 时,求
时,求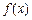 在闭区间
在闭区间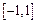 上的最大值与最小值;
上的最大值与最小值;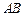 :
: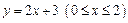 与导函数
与导函数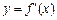 的图像只有一个交点,且交点在线段
的图像只有一个交点,且交点在线段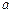 的取值范围.
的取值范围.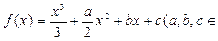 R),函数
R),函数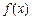 的导数记为
的导数记为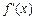 .
.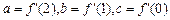 ,求a、b、c的值;
,求a、b、c的值;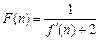 ,求证:F(1)+ F(2)+ F(3)+…+ F(n)<
,求证:F(1)+ F(2)+ F(3)+…+ F(n)<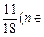 N*);
N*);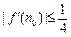 ?说明理由.
?说明理由.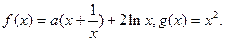
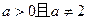 ,直线l与函数
,直线l与函数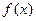 和函数
和函数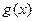 的图象相切于一点,求切线l的方程。
的图象相切于一点,求切线l的方程。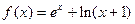 (其中常数e为自然对数的底数),则
(其中常数e为自然对数的底数),则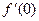 = .
= .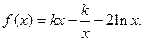
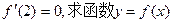 的解析式;
的解析式;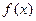 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数 的取值范围.
的取值范围.