题目内容
(本小题满分12分)
设函数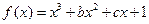 的单调减区间是(1,2)
的单调减区间是(1,2)
⑴求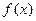 的解析式;
的解析式;
⑵若对任意的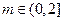 ,关于
,关于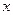 的不等式
的不等式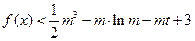 在
在
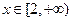 时有解,求实数
时有解,求实数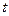 的取值范围.
的取值范围.
设函数
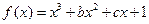 的单调减区间是(1,2)
的单调减区间是(1,2)⑴求
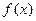 的解析式;
的解析式;⑵若对任意的
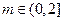 ,关于
,关于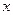 的不等式
的不等式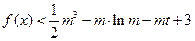 在
在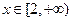 时有解,求实数
时有解,求实数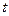 的取值范围.
的取值范围.解:⑴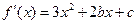 .
.
∵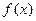 的单调减区间是(1,2),∴
的单调减区间是(1,2),∴ ,………3分
,………3分
∴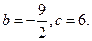
∴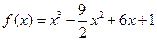 . ………5分
. ………5分
⑵由⑴得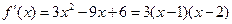 ,
,
当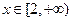 时,
时, ≥0,∴
≥0,∴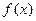 在
在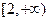 单调递增,
单调递增,
∴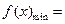
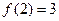 .
.
要使关于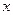 的不等式
的不等式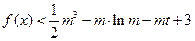 在
在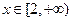 时有解,
时有解,
即
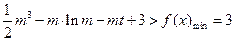 , ………7分
, ………7分
即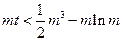 对任意
对任意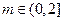 恒成立,
恒成立,
只需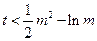 在
在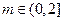 恒
恒 成立.
成立.
设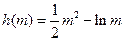 ,
,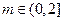 ,则
,则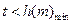 . ………9分
. ………9分
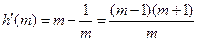 ,
,
当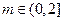 时,
时,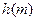 在
在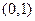 上递减,在
上递减,在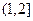 上递增,:]
上递增,:]
∴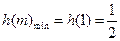 .
.
∴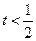 . ………12分
. ………12分
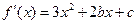 .
.∵
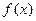 的单调减区间是(1,2),∴
的单调减区间是(1,2),∴ ,………3分
,………3分∴
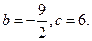
∴
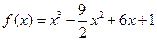 . ………5分
. ………5分⑵由⑴得
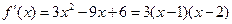 ,
,当
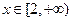 时,
时, ≥0,∴
≥0,∴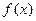 在
在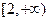 单调递增,
单调递增,∴
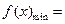
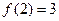 .
.要使关于
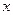 的不等式
的不等式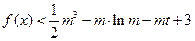 在
在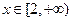 时有解,
时有解,即

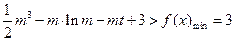 , ………7分
, ………7分即
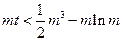 对任意
对任意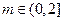 恒成立,
恒成立,只需
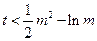 在
在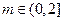 恒
恒 成立.
成立.设
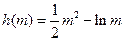 ,
,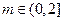 ,则
,则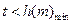 . ………9分
. ………9分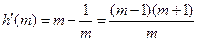 ,
,当
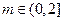 时,
时,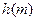 在
在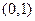 上递减,在
上递减,在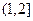 上递增,:]
上递增,:]∴
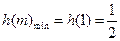 .
.∴
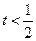 . ………12分
. ………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
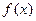 是定义在
是定义在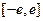 上的奇函数,当
上的奇函数,当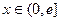 时
时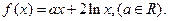
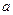 ,使得当
,使得当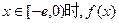 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出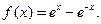
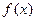 的导数
的导数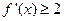 ;
;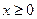 都有
都有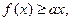 求a的取值范围。
求a的取值范围。 x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0. )求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.
)求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.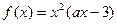 ,其中a为常数.
,其中a为常数.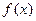 的一个极值点,求a的值;
的一个极值点,求a的值;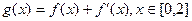 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.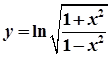 的导数为 。
的导数为 。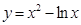 上的任意一点,则点P到直线
上的任意一点,则点P到直线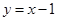 的最小距离为 ▲
的最小距离为 ▲