题目内容
12.若非零向量$\overrightarrow a,\overrightarrow b$满足$|\overrightarrow a+\overrightarrow b|=|\overrightarrow a-\overrightarrow b|=2|\overrightarrow b|$,则$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$的夹角是60°.分析 根据已知等式,利用平面向量的平行四边形法则计算,判断即可得到结果.
解答 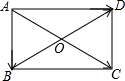 解:如图所示,|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,得到平行四边形对角线相等,即四边形ABCD为矩形,
解:如图所示,|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,得到平行四边形对角线相等,即四边形ABCD为矩形,
∵|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=2|$\overrightarrow{b}$|,
得到对角线是矩形一边长的2倍,
则|$\overrightarrow{a}$+$\overrightarrow{b}$|与|$\overrightarrow{a}$-$\overrightarrow{b}$|的夹角是60°,
故答案为:60°
点评 此题考查了平面向量的数量积的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
3.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(e)+lnx,则f′(e)=( )
| A. | 1 | B. | -1 | C. | -e-1 | D. | -e |
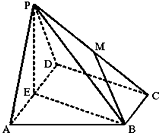 如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,PA=PD=4,BC=$\frac{1}{2}$AD=2,CD=2$\sqrt{3}$.
如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,PA=PD=4,BC=$\frac{1}{2}$AD=2,CD=2$\sqrt{3}$.