题目内容
17.关于函数f(x)=sin(2x-$\frac{π}{6}$)(x∈R),给出下列三个结论:①函数f(x)的图象与g(x)=cos(2x-$\frac{2π}{3}$)的图象重合;
②函数f(x)的图象关于点($\frac{π}{12}$,0)对称;
③函数f(x)的图象关于直线x=$\frac{π}{3}$对称.
其中正确的个数是( )
| A. | 0个 | B. | 1个 | C. | 3个 | D. | 2个 |
分析 ①根据三角函数的图象关系进行判断.
②根据三角函数的对称性进行判断.
③根据三角函数的对称性进行判断.
解答 解:①函数f(x)=sin(2x-$\frac{π}{6}$)=cos[$\frac{π}{2}$-(2x-$\frac{π}{6}$)]=cos($\frac{2π}{3}$-2x)=cos(2x-$\frac{2π}{3}$),故①正确;
②f($\frac{π}{12}$)=sin(2×$\frac{π}{12}$-$\frac{π}{6}$)=sin($\frac{π}{6}$-$\frac{π}{6}$)=sin0=0,即函数f(x)的图象关于点($\frac{π}{12}$,0)对称成立,故②正确;
③f($\frac{π}{3}$)=sin(2×$\frac{π}{3}$-$\frac{π}{6}$)=sin$\frac{π}{2}$=1为最大值,即函数f(x)的图象关于直线x=$\frac{π}{3}$对称成立,故③正确,
综上正确的个数3个,
故选:C
点评 本题主要考查与三角函数有关的图象和性质,根据三角函数的对称性是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知△ABC的三边长分别为AB=$\sqrt{{m}^{2}+{n}^{2}}$,AC=$\sqrt{{m}^{2}+{t}^{2}}$,BC=$\sqrt{{n}^{2}+{t}^{2}}$,其中m,n,t∈(0,+∞),则△ABC是( )
| A. | 直角三角形 | B. | 钝角三角形 | ||
| C. | 锐角三角形 | D. | 以上三种情况都有可能 |
20.某程序框图如图所示,则输出的结果为( )
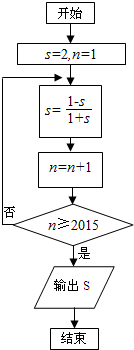

| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{3}$ | D. | -3 |