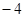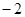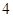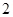题目内容
已知F是双曲线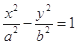 的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且
的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且 ,则此双曲线的离心率为( ).
,则此双曲线的离心率为( ).
A .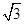 B.
B.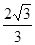 C.
C. 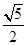 D.
D.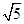
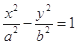 的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且
的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且 ,则此双曲线的离心率为( ).
,则此双曲线的离心率为( ).A .
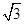 B.
B.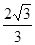 C.
C. 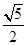 D.
D.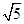
B.
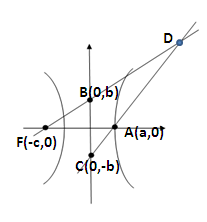
试题分析:如图,由已知可得直线FB的方程为:
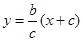 ,直线AC的方程为:
,直线AC的方程为: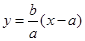 ,联立前两方程可得D点坐标为:
,联立前两方程可得D点坐标为: ,因此有
,因此有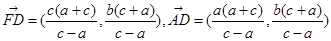 ,又
,又 ,所以有
,所以有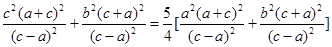 ,整理得
,整理得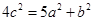 ,又
,又 ,所以有:
,所以有: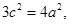 即
即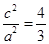 ,故
,故 .
.

练习册系列答案
相关题目
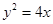 的焦点为顶点,顶点为中心,离心率为2的双曲线方程是 .
的焦点为顶点,顶点为中心,离心率为2的双曲线方程是 . 中,已知中心在坐标原点的双曲线
中,已知中心在坐标原点的双曲线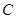 经过点
经过点 ,且它的右焦点
,且它的右焦点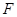 与抛物线
与抛物线 的焦点相同,则该双曲线的标准方程为 .
的焦点相同,则该双曲线的标准方程为 . 的左焦点
的左焦点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,双曲线左顶点为
,双曲线左顶点为 ,若
,若 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )

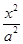 -y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )
-y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )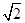 B.
B.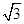 C.2 D.
C.2 D.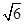
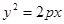 的焦点与双曲线
的焦点与双曲线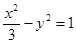 的右焦点重合,则p的值为( )
的右焦点重合,则p的值为( )