题目内容
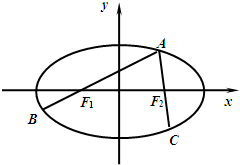
如图,A为椭圆
+
=1(a>b>0)上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,恰好有AF1:AF2=3:1.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设
=λ1
,
=λ2
.
①当A点恰为椭圆短轴的一个端点时,求λ1+λ2的值;
②当A点为该椭圆上的一个动点时,试判断是λ1+λ2否为定值?若是,请证明;若不是,请说明理由.
| x2 |
| a2 |
| y2 |
| b1 |
(Ⅰ)求椭圆的离心率;
(Ⅱ)设
| AF1 |
| F1B |
| AF2 |
| F2C |
①当A点恰为椭圆短轴的一个端点时,求λ1+λ2的值;
②当A点为该椭圆上的一个动点时,试判断是λ1+λ2否为定值?若是,请证明;若不是,请说明理由.

(Ⅰ)设|AF1|=m,则|AF2|=3m.
由题设及椭圆定义得
,
消去m得a2=2c2,所以离心率
.
(Ⅱ)设A(x0,y0),B(x1,y1),C(x2,y2),
则
=(-C-x0,-y0),
B=(x1+C,y1)
∵
=λ1
,∴x1=-
-c,y1=-
又x02+2y02=2c2①,x12+2y12=2c2②,
将x1,y1代入②得:
(
+c)2+2(
)2=2c2即(c+x0+cλ1)2=2y20=2λ1c2③;
③-①得:2x0=cλ1-3c;
同理:由
=λ2
.得2x0=-cλ2+3c;
∴cλ1-3c=-cλ2+3c,
∴λ1+λ2=6.
由题设及椭圆定义得
|
消去m得a2=2c2,所以离心率
| ||
| 2 |
(Ⅱ)设A(x0,y0),B(x1,y1),C(x2,y2),
则
| AF1 |
| F1 |
∵
| AF1 |
| F1B |
| c+x0 |
| λ1 |
| y0 |
| λ1 |
又x02+2y02=2c2①,x12+2y12=2c2②,
将x1,y1代入②得:
(
| c+x0 |
| λ1 |
| y0 |
| λ1 |
③-①得:2x0=cλ1-3c;
同理:由
| AF2 |
| F2C |
∴cλ1-3c=-cλ2+3c,
∴λ1+λ2=6.

练习册系列答案
相关题目
 的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且
的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且 ,则此双曲线的离心率为( ).
,则此双曲线的离心率为( ). B.
B. C.
C.  D.
D.
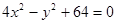 上的一点
上的一点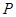 到一个焦点的距离等于1,那么点
到一个焦点的距离等于1,那么点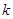 满足
满足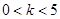 ,则曲线
,则曲线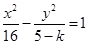 与曲线
与曲线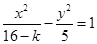 的( )
的( )