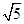题目内容
设F1、F2分别为椭圆C:
+
=1(a>0,b>0)的左、右焦点,椭圆上一点M满足∠MF1O=
,N为MF1的中点且ON⊥MF1,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
A.
| B.
| C.2-
| D.
|
连接MF2,则ON是△MF1F2的中位线,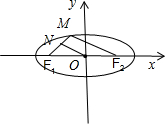
∴|NF1|+|NO|=
(|MF1|+|MF2|)=a,
又∵∠MF1O=
,|OF1|=c,且ON⊥MF1,
∴|NF1|=
c,|NO|=
c,
∴
c+
c=a,
解得e=
=
=
-1.
故选:A.

∴|NF1|+|NO|=
| 1 |
| 2 |
又∵∠MF1O=
| π |
| 3 |
∴|NF1|=
| 1 |
| 2 |
| ||
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
解得e=
| c |
| a |
| 2 | ||
1+
|
| 3 |
故选:A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
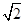 ,且过点(4,-
,且过点(4,-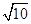 ).
).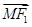 ·
· =0;
=0;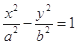 的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且
的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且 ,则此双曲线的离心率为( ).
,则此双曲线的离心率为( ).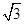 B.
B.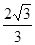 C.
C. 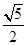 D.
D.