题目内容
已知a,b是单位向量,a·b=0.若向量c满足|c-a-b|=1,则|c|的最大值为( )
A.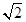 -1 -1 | B.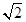 |
C.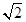 +1 +1 | D.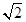 +2 +2 |
C
因为a,b是单位向量,且a·b=0,
可令a=(1,0),b=(0,1),设向量c=(x,y),
则c-a-b=(x,y)-(1,0)-(0,1)=(x-1,y-1),
|c-a-b|=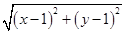 ,
,
又|c-a-b|=1,
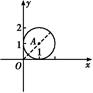
所以(x-1)2+(y-1)2=1,圆心A为(1,1),半径为1.
如图,|c|的最大值表示原点到圆上动点的最大值,
|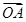 |=
|=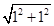 =
=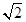 ,
,
|c|的最大值为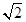 +1.故选C.
+1.故选C.
可令a=(1,0),b=(0,1),设向量c=(x,y),
则c-a-b=(x,y)-(1,0)-(0,1)=(x-1,y-1),
|c-a-b|=
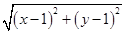 ,
,又|c-a-b|=1,
所以(x-1)2+(y-1)2=1,圆心A为(1,1),半径为1.
如图,|c|的最大值表示原点到圆上动点的最大值,

|
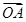 |=
|=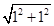 =
=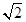 ,
,|c|的最大值为
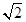 +1.故选C.
+1.故选C.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
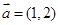 ,
,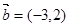 ,当
,当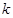 为何值时,
为何值时,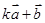 与
与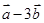 垂直?(2)
垂直?(2)
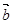 与
与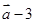
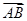 ="(cos" 18°,cos 72°),
="(cos" 18°,cos 72°), 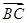 ="(2cos" 63°,2cos 27°),则△ABC面积为( )
="(2cos" 63°,2cos 27°),则△ABC面积为( )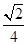

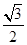
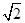
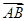 在
在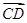 方向上的投影为( )
方向上的投影为( )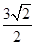

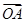 +
+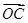 =-2
=-2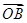 ,则△AOB与△AOC的面积之比为________.
,则△AOB与△AOC的面积之比为________.
 和
和 ,定义
,定义 ,若平面向量
,若平面向量 满足:
满足: ,
, 与
与 的夹角
的夹角 ,且
,且 和
和 都在集合
都在集合 中,则
中,则 .
. ,
,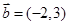 ,若
,若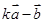 与
与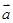 垂直,则实数
垂直,则实数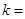 ( )
( )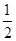
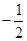
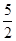
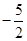
 =a,
=a, =b,
=b, =c,则下列向量中与
=c,则下列向量中与 相等的向量是( )
相等的向量是( )
 a+
a+