题目内容
9．
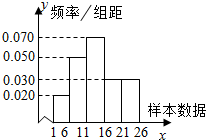已知儿童退烧药，其药品安全性疑虑引起社会的广泛关注，国家药监局调查了这种的100个相关数据，绘制成如图所示的频率分布直方图，则估计样本数据的中位数为（精确到0.01）（ ）| A． | 13.5 | B． | 13.14 | C． | 13.25 | D． | 13.34 |
分析 设中位数为x，根据已知中的频率分布直方图，计算能使图中矩形面积平分的x值，可得答案．
解答 解：根据前两组的累积频率为（0.020+0.050）×5=0.35＜0.5，
前三组的累积频率为（0.020+0.050+0.070）×5=0.7＞0.5，
故中位数位于第三组，设中位数为x，
则（x-11）×0.070+（0.020+0.050）×5=0.5，
解得：x=11+$\frac{15}{7}$≈13.14，
故选：B
点评 本题考查的知识点是频率分布直方图，难度不大，属于基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
1．已知等式$sin（θ+\frac{π}{6}）=1-{log_{\frac{1}{2}}}x$，则x的取值范围是（ ）
| A． | [1，4] | B． | $[{\frac{1}{4}，1}]$ | C． | [2，4] | D． | $[{\frac{1}{4}，4}]$ |
18．当0＜x＜1时，下列不等式成立的是（ ）
| A． | （$\frac{1}{2}$）x+1＞（$\frac{1}{2}$）1-x | B． | log（1+x）（1-x）＞1 | C． | 0＜1-x2＜1 | D． | log（1-x）（1+x）＞0 |
19．设点A（-1，0），B（1，0），动点P到A点的距离与到B点的距离之比为2，则点P的轨迹方程是（ ）
| A． | ${（x-\frac{5}{3}）^2}+{y^2}=\frac{16}{9}$ | B． | ${（x+\frac{5}{3}）^2}+{y^2}=\frac{16}{9}$ | C． | ${（x-\frac{5}{3}）^2}+{y^2}=\frac{4}{3}$ | D． | ${（x+\frac{5}{3}）^2}+{y^2}=\frac{4}{3}$ |