题目内容
5.计算下列各题:(1)$\frac{1}{2}$lg$\frac{32}{49}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{245}$
(2)lg25+lg2×lg50+lg22.
分析 (1)由已知条件利用对数的性质、运算法则求解.
(2)由已知条件利用对数的性质、运算法则求解.
解答 解:(1)$\frac{1}{2}$lg$\frac{32}{49}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{245}$
=lg$\frac{4\sqrt{2}}{7}$-lg4+lg$7\sqrt{5}$
=lg($\frac{4\sqrt{2}}{7}×\frac{1}{4}×7\sqrt{5}$)
=lg$\sqrt{10}$
=$\frac{1}{2}$.
(2)lg25+lg2×lg50+lg22
=2lg5+lg2(2lg5+lg2)+lg22
=2lg5+2lg2lg5+2lg22
=2lg5+2lg2(lg5+lg2)
=2(lg5+lg2)
=2.
点评 本题考查对数式化简求值,是基础题,解题时要认真审题,注意对数的性质、运算法则的合理运用.

练习册系列答案
相关题目
14.已知函数f(x)=-x+log2$\frac{1-x}{1+x}$.
(1)求函数f(x)的定义域;
(2)当x∈[-$\frac{1}{2}$,$\frac{1}{2}$]时,求f(x)的最大值.
(1)求函数f(x)的定义域;
(2)当x∈[-$\frac{1}{2}$,$\frac{1}{2}$]时,求f(x)的最大值.
9.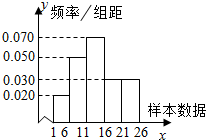 已知儿童退烧药,其药品安全性疑虑引起社会的广泛关注,国家药监局调查了这种的100个相关数据,绘制成如图所示的频率分布直方图,则估计样本数据的中位数为(精确到0.01)( )
已知儿童退烧药,其药品安全性疑虑引起社会的广泛关注,国家药监局调查了这种的100个相关数据,绘制成如图所示的频率分布直方图,则估计样本数据的中位数为(精确到0.01)( )
 已知儿童退烧药,其药品安全性疑虑引起社会的广泛关注,国家药监局调查了这种的100个相关数据,绘制成如图所示的频率分布直方图,则估计样本数据的中位数为(精确到0.01)( )
已知儿童退烧药,其药品安全性疑虑引起社会的广泛关注,国家药监局调查了这种的100个相关数据,绘制成如图所示的频率分布直方图,则估计样本数据的中位数为(精确到0.01)( )| A. | 13.5 | B. | 13.14 | C. | 13.25 | D. | 13.34 |