题目内容
19．设点A（-1，0），B（1，0），动点P到A点的距离与到B点的距离之比为2，则点P的轨迹方程是（ ）| A． | ${（x-\frac{5}{3}）^2}+{y^2}=\frac{16}{9}$ | B． | ${（x+\frac{5}{3}）^2}+{y^2}=\frac{16}{9}$ | C． | ${（x-\frac{5}{3}）^2}+{y^2}=\frac{4}{3}$ | D． | ${（x+\frac{5}{3}）^2}+{y^2}=\frac{4}{3}$ |
分析 设点P（x，y），由题意可知：|PA|=2|PB|，由两点间的距离公式化简可得轨迹E的方程．
解答 解：设点P（x，y），由题意可知：|PA|=2|PB|，则$\sqrt{（x+1）^{2}+{y}^{2}}$=2$\sqrt{（x-1）^{2}+{y}^{2}}$，
故P点的轨迹E的方程为：${（x-\frac{5}{3}）^2}+{y^2}=\frac{16}{9}$．
故选：A．
点评 本题考查求点的轨迹方程的方法，正确化简是解题的关键．
练习册系列答案
相关题目
9．
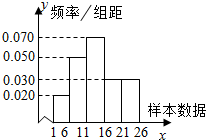已知儿童退烧药，其药品安全性疑虑引起社会的广泛关注，国家药监局调查了这种的100个相关数据，绘制成如图所示的频率分布直方图，则估计样本数据的中位数为（精确到0.01）（ ）
已知儿童退烧药，其药品安全性疑虑引起社会的广泛关注，国家药监局调查了这种的100个相关数据，绘制成如图所示的频率分布直方图，则估计样本数据的中位数为（精确到0.01）（ ）| A． | 13.5 | B． | 13.14 | C． | 13.25 | D． | 13.34 |
10．数列{$\frac{2n}{n-4π}$}中的最大项是（ ）
| A． | 第11项 | B． | 第12项 | C． | 第13项 | D． | 第14项 |
14．已知sin（π+θ）+cos（$\frac{π}{2}$+θ）=-2$\sqrt{3}$cos（2π-θ），则sinθcosθ-cos2θ=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}-1}{4}$ | D． | $\frac{1-\sqrt{3}}{4}$ |
4．一商场对每天进店人数和商品销售件数进行了统计对比，得到如下表格：
其中i=1，2，3，4，5，6，7．
（1）以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图；
（2）求回归直线方程．（结果保留到小数点后两位）
参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$
（3）预测进店人数为80人时，商品销售的件数．（结果保留整数）
| 人数xi | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 件数yi | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
（1）以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图；
（2）求回归直线方程．（结果保留到小数点后两位）
参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$
（3）预测进店人数为80人时，商品销售的件数．（结果保留整数）
11．函数f（x）=2cos（ωx+$\frac{π}{3}$）（ω＞0）的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列，要得到函数g（x）=2sinωx的图象，只需将函数f（x）的图象（ ）
| A． | 向左平移$\frac{π}{12}$个单位长度 | B． | 向右平移$\frac{π}{6}$个单位长度 | ||
| C． | 向右平移$\frac{5π}{12}$个单位长度 | D． | 向左平移$\frac{π}{3}$个单位长度 |