题目内容
14．当复数z=$\frac{1}{m+5}+（{m^2}+2m-15）i$为实数时，实数m=3．分析 利用复数的虚部为0，实部有意义，求解即可．
解答 解：复数z=$\frac{1}{m+5}+（{m^2}+2m-15）i$为实数时，
可得m2+2m-15=0，解得m=3或m=-5（舍去）
故答案为：3．
点评 本题考查复数的基本概念，是基础题，注意实部有意义是易错点．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
9．
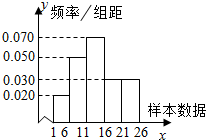已知儿童退烧药，其药品安全性疑虑引起社会的广泛关注，国家药监局调查了这种的100个相关数据，绘制成如图所示的频率分布直方图，则估计样本数据的中位数为（精确到0.01）（ ）
已知儿童退烧药，其药品安全性疑虑引起社会的广泛关注，国家药监局调查了这种的100个相关数据，绘制成如图所示的频率分布直方图，则估计样本数据的中位数为（精确到0.01）（ ）| A． | 13.5 | B． | 13.14 | C． | 13.25 | D． | 13.34 |
19．设a=sin55°，b=cos55°，c=tan55°，则（ ）
| A． | a＞b＞c | B． | b＞c＞a | C． | c＞a＞b | D． | c＞b＞a |
4．一商场对每天进店人数和商品销售件数进行了统计对比，得到如下表格：
其中i=1，2，3，4，5，6，7．
（1）以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图；
（2）求回归直线方程．（结果保留到小数点后两位）
参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$
（3）预测进店人数为80人时，商品销售的件数．（结果保留整数）
| 人数xi | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 件数yi | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
（1）以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图；
（2）求回归直线方程．（结果保留到小数点后两位）
参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$
（3）预测进店人数为80人时，商品销售的件数．（结果保留整数）