题目内容
1.已知等式$sin(θ+\frac{π}{6})=1-{log_{\frac{1}{2}}}x$,则x的取值范围是( )| A. | [1,4] | B. | $[{\frac{1}{4},1}]$ | C. | [2,4] | D. | $[{\frac{1}{4},4}]$ |
分析 由正弦函数的值域可得关于x的不等式,结合对数函数的性质可得.
解答 解:∵$sin(θ+\frac{π}{6})=1-{log_{\frac{1}{2}}}x$,sin(θ+$\frac{π}{6}$)∈[-1,1],
∴-1≤1-$lo{g}_{\frac{1}{2}}x$≤1,∴0≤$lo{g}_{\frac{1}{2}}x$≤2,
由对数函数可得$\frac{1}{4}$≤x≤1,
故选:B
点评 本题考查正弦函数的值域,涉及对数函数的性质,属基础题.

练习册系列答案
相关题目
9.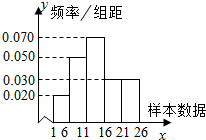 已知儿童退烧药,其药品安全性疑虑引起社会的广泛关注,国家药监局调查了这种的100个相关数据,绘制成如图所示的频率分布直方图,则估计样本数据的中位数为(精确到0.01)( )
已知儿童退烧药,其药品安全性疑虑引起社会的广泛关注,国家药监局调查了这种的100个相关数据,绘制成如图所示的频率分布直方图,则估计样本数据的中位数为(精确到0.01)( )
 已知儿童退烧药,其药品安全性疑虑引起社会的广泛关注,国家药监局调查了这种的100个相关数据,绘制成如图所示的频率分布直方图,则估计样本数据的中位数为(精确到0.01)( )
已知儿童退烧药,其药品安全性疑虑引起社会的广泛关注,国家药监局调查了这种的100个相关数据,绘制成如图所示的频率分布直方图,则估计样本数据的中位数为(精确到0.01)( )| A. | 13.5 | B. | 13.14 | C. | 13.25 | D. | 13.34 |
16.若tanx<0,则( )
| A. | sinx<0 | B. | cosx<0 | C. | sin2x<0 | D. | cos2x<0 |
10.数列{$\frac{2n}{n-4π}$}中的最大项是( )
| A. | 第11项 | B. | 第12项 | C. | 第13项 | D. | 第14项 |
11.函数f(x)=2cos(ωx+$\frac{π}{3}$)(ω>0)的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,要得到函数g(x)=2sinωx的图象,只需将函数f(x)的图象( )
| A. | 向左平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{5π}{12}$个单位长度 | D. | 向左平移$\frac{π}{3}$个单位长度 |