题目内容
已知抛物线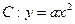 ,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
(I)求抛物线C的焦点坐标;
(II)若点M满足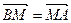 ,求点M的轨迹方程.
,求点M的轨迹方程.
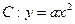 ,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.(I)求抛物线C的焦点坐标;
(II)若点M满足
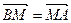 ,求点M的轨迹方程.
,求点M的轨迹方程.(Ⅰ)焦点坐标为F(0,-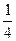 )
)
(Ⅱ)M的轨迹方程为: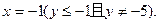
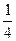 )
)(Ⅱ)M的轨迹方程为:
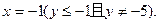
(I)将P(1,-1)代入抛物线C的方程
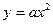 得a=-1,
得a=-1,∴抛物线C的方程为
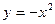 ,即
,即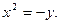
焦点坐标为F(0,-
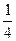 ).……………………………………4分
).……………………………………4分(II)设直线PA的方程为
 ,
,联立方程
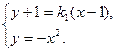 消去y得
消去y得
则
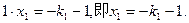
由
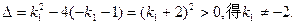 ………………7分
………………7分同理直线PB的方程为
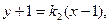
联立方程
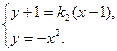 消去y得
消去y得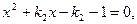
则
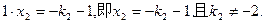
又
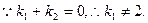 …………………………9分
…………………………9分设点M的坐标为(x,y),由
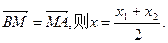

又
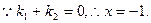 …………………………………………11分
…………………………………………11分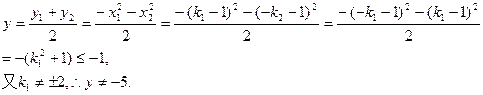
∴所求M的轨迹方程为:
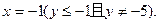

练习册系列答案
相关题目
 ,直线
,直线 :
: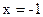 ,
, 为平面上的动点,过点
为平面上的动点,过点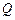 ,且
,且 .(1)求动点
.(1)求动点 轨迹
轨迹 的方程;
的方程; ,试推断:动直线DE是否过定点?证明你的结论。
,试推断:动直线DE是否过定点?证明你的结论。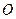 为原点的直角坐标系中,点
为原点的直角坐标系中,点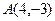 为
为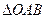 的直角顶点,若
的直角顶点,若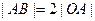 ,且点
,且点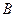 的纵坐标大于0
的纵坐标大于0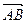 的坐标;
的坐标;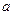 ,使得抛物线
,使得抛物线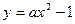 上总有关于直线
上总有关于直线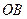 对称的两个点?若存在,求实数
对称的两个点?若存在,求实数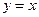 对称,则C2的准线方程是 .
对称,则C2的准线方程是 .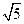 ,求此抛物线的标准方程.
,求此抛物线的标准方程. 上有一点
上有一点 ,它到焦点的距离等于
,它到焦点的距离等于 ,求实数
,求实数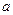 与
与 的值.
的值.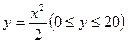 ,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________. 的准线方程是 ;
的准线方程是 ;