题目内容
(本小题满分13分)已知点 ,直线
,直线 :
: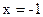 ,
, 为平面上的动点,过点
为平面上的动点,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为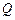 ,且
,且 .(1)求动点
.(1)求动点 的
的 轨迹
轨迹 的方程;
的方程;
(2)已知点A(m,2)在曲线C上,过点A作曲线C的两条弦AD,AE,且AD,AE的斜率k1、k2满足 ,试推断:动直线DE是否过定点?证明你的结论。
,试推断:动直线DE是否过定点?证明你的结论。
 ,直线
,直线 :
: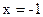 ,
, 为平面上的动点,过点
为平面上的动点,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为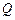 ,且
,且 .(1)求动点
.(1)求动点 的
的 轨迹
轨迹 的方程;
的方程;(2)已知点A(m,2)在曲线C上,过点A作曲线C的两条弦AD,AE,且AD,AE的斜率k1、k2满足
 ,试推断:动直线DE是否过定点?证明你的结论。
,试推断:动直线DE是否过定点?证明你的结论。(1)动点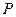 的轨迹
的轨迹
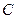 的方程
的方程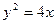 (2)
(2)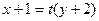 直线DE过定点(-1,-2)
直线DE过定点(-1,-2)
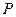 的轨迹
的轨迹
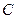 的方程
的方程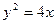 (2)
(2)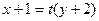 直线DE过定点(-1,-2)
直线DE过定点(-1,-2)(1)设
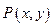 ,则
,则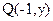 ,
, ∵
∵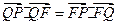 ,
,
∴ .
. 
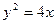 ,
,
所以动点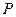 的轨迹
的轨迹
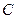 的方程
的方程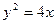 .
.  ………5分
………5分
(2)将A(m,2)代入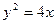 得m="1," ∴A(1,2) …………………………6分
得m="1," ∴A(1,2) …………………………6分
法一: ∵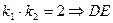 两点不可能关于x轴对称,∴DE不斜率必存在
两点不可能关于x轴对称,∴DE不斜率必存在
设直线DE的方程为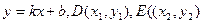
由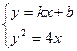 得
得
∴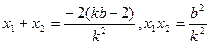 ………………………8分
………………………8分
∵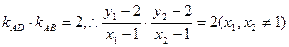 且
且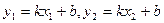
∴ …………………9分
…………………9分
将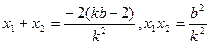 代入化简得
代入化简得
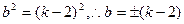 …………………………………10分
…………………………………10分
将b=k-2代入y=kx+b得y =kx+k-2=k(x+1)-2,过定点(-1,-
=kx+k-2=k(x+1)-2,过定点(-1,- 2)…………11分
2)…………11分
将b=2-k代入y=kx+b
得y=kx +2-k=k(x-1)+2,过定点(1,2)即为A点,舍去
+2-k=k(x-1)+2,过定点(1,2)即为A点,舍去
∴直线DE过定点(-1,-2) …………………………………………13分
法二 :设
:设 ,(5分)
,(5分) 则
则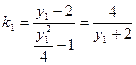
 ……7分
……7分
同理
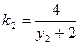 ,由已知得
,由已知得
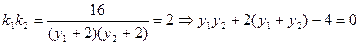 …………9分
…………9分
设直线DE的方程为x=ty+n代入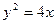
得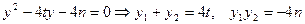 …………10分
…………10分
∴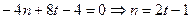 ,直线DE的方程为
,直线DE的方程为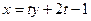 …12分
…12分
即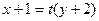 直线DE过定点(-1,-2) ………13分
直线DE过定点(-1,-2) ………13分

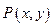 ,则
,则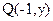 ,
, ∵
∵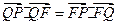 ,
,∴
 .
. 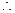
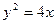 ,
,所以动点
 的轨迹
的轨迹
 的方程
的方程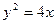 .
.  ………5分
………5分(2)将A(m,2)代入
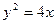 得m="1," ∴A(1,2) …………………………6分
得m="1," ∴A(1,2) …………………………6分法一: ∵
 两点不可能关于x轴对称,∴DE不斜率必存在
两点不可能关于x轴对称,∴DE不斜率必存在设直线DE的方程为
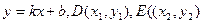
由
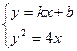 得
得
∴
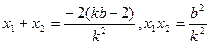 ………………………8分
………………………8分∵
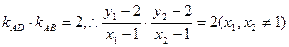 且
且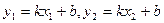
∴
 …………………9分
…………………9分将
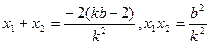 代入化简得
代入化简得 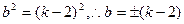 …………………………………10分
…………………………………10分将b=k-2代入y=kx+b得y
 =kx+k-2=k(x+1)-2,过定点(-1,-
=kx+k-2=k(x+1)-2,过定点(-1,- 2)…………11分
2)…………11分将b=2-k代入y=kx+b
得y=kx
 +2-k=k(x-1)+2,过定点(1,2)即为A点,舍去
+2-k=k(x-1)+2,过定点(1,2)即为A点,舍去∴直线DE过定点(-1,-2) …………………………………………13分
法二
 :设
:设 ,(5分)
,(5分) 则
则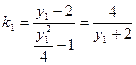
 ……7分
……7分同理

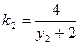 ,由已知得
,由已知得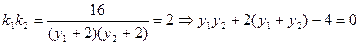 …………9分
…………9分设直线DE的方程为x=ty+n代入
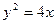
得
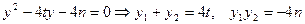 …………10分
…………10分∴
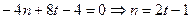 ,直线DE的方程为
,直线DE的方程为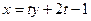 …12分
…12分即
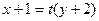 直线DE过定点(-1,-2) ………13分
直线DE过定点(-1,-2) ………13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
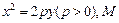 直线
直线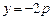 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。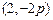 时,
时,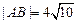 ,求此时抛物线的方程;
,求此时抛物线的方程;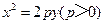 上,其中,点C满足
上,其中,点C满足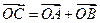 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.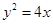 上的两点A、B满足
上的两点A、B满足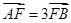 ,则弦AB的中点到准线的距离为___________.
,则弦AB的中点到准线的距离为___________.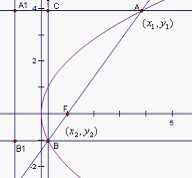
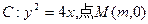 在x轴的正半轴上,过M的直线
在x轴的正半轴上,过M的直线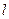 与C相交于A、B两点,O为坐标原点。
与C相交于A、B两点,O为坐标原点。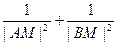 恒为定值。
恒为定值。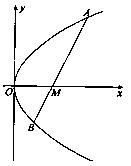
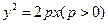 的焦点与椭圆
的焦点与椭圆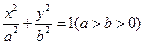 的一个焦点重合,且抛物线与椭圆的一个交点为
的一个焦点重合,且抛物线与椭圆的一个交点为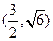 ,(1)求抛物线与椭圆的方程,(2)若过点
,(1)求抛物线与椭圆的方程,(2)若过点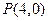 的直线与抛物线交于点
的直线与抛物线交于点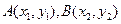 ,求
,求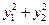 的最小值
的最小值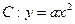 ,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.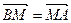 ,求点M的轨迹方程.
,求点M的轨迹方程.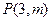 在以点
在以点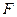 为焦点的抛物线
为焦点的抛物线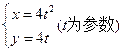 上,则
上,则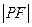 等于 .
等于 .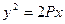 的一条焦点弦AB被焦点F分成长为m、n的两部分,求证:
的一条焦点弦AB被焦点F分成长为m、n的两部分,求证: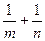 为定值
为定值 如图,F是抛物线
如图,F是抛物线 的焦点,Q为准线与
的焦点,Q为准线与 轴的交点,直线
轴的交点,直线 经过点Q.
经过点Q. ,
, .求证:
.求证: 为定值.
为定值.