Question

5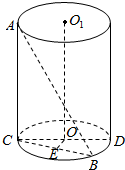．如图，AC为圆柱的母线，CD为底面直径，线段AB的两个端点分别在上、下底面圆周上，它与圆周的轴OO₁之间的距离为3，所成角为30°，且AB=16，求此圆柱的侧面积．

Answer 1

分析 根据已知求出圆柱的底面半径和高，代入圆柱的侧面积公式，可得答案．

解答 解：∵异面直线AB与轴OO₁的夹角为30°，
AC∥OO₁，
故直线AB与AC的夹角为30°，
∵AB=16，
故AC=8$\sqrt{3}$，BC=8，
又由AB与轴OO₁的距离为3，
故OE=3，
则OB=OC=5，
即圆柱的底面半径为5，高为8$\sqrt{3}$，
故圆柱的侧面积S=2×$5×8\sqrt{3}×π$=80$\sqrt{3}π$

点评 本题考查的知识点是旋转体，根据已知求出圆柱的底面半径和高，是解答的关键．