题目内容
11.已知集合A={x|x2-5x+4≤0},B={x|x2-2ax+a+2<0},若B⊆A,求a的取值范围.分析 分别解出集合A、B,对于集合B,我们需要讨论它是不是空集,再根据子集的定义进行求解
解答 解:集合A={x|x2-5x+4≤0},集合B={x|x2-2ax+a+2≤0},
B⊆A,解得A={x|1≤x≤4},
若B≠∅,△=(-2a)2-4(a+2)=4a2-4a-8≥0,
可得a≥2或a≤-1;
B={x|a-$\sqrt{{a}^{2}-a-2}$<x<a+$\sqrt{{a}^{2}-a-2}$},
∵B⊆A,
∴a+$\sqrt{{a}^{2}-a-2}$≤4①,a-$\sqrt{{a}^{2}-a-2}$≥1,
解不等式①得,a≤$\frac{18}{7}$,
解不等式②得,1≤a≤3,取交集得,1≤a≤$\frac{18}{7}$,
又∵△≥0,可得a≥2或a≤-1;
可得2≤a≤$\frac{18}{7}$
若B=∅,可得△=(-2a)2-4(a+2)=4a2-4a-8<0,解得-1<a<2;
综上可取并集得:-1<a≤$\frac{18}{7}$.
点评 本题考点集合关系中的参数取值问题,考查了一元二次不等式的解法,集合包含关系的判断,解题的本题,关键是理解B⊆A,由此得出应分两类求参数,忘记分类是本题容易出错的一个原因,在做包含关系的题时,一定要注意空集的情况,莫忘记讨论空集导致错误.

练习册系列答案
相关题目
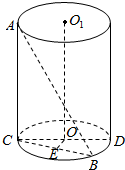 如图,AC为圆柱的母线,CD为底面直径,线段AB的两个端点分别在上、下底面圆周上,它与圆周的轴OO1之间的距离为3,所成角为30°,且AB=16,求此圆柱的侧面积.
如图,AC为圆柱的母线,CD为底面直径,线段AB的两个端点分别在上、下底面圆周上,它与圆周的轴OO1之间的距离为3,所成角为30°,且AB=16,求此圆柱的侧面积.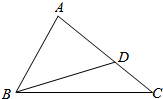 如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.
如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.