题目内容
14.已知抛物线y2=4x的焦点为F,准线为l,点P(x0,y0)(y0>0)在其上,线段PF与抛物线交于点Q,若$\overrightarrow{PQ}$=3$\overrightarrow{QF}$,则直线PF的斜率为-2$\sqrt{2}$.分析 利用抛物线的定义,结合$\overrightarrow{PQ}$=3$\overrightarrow{QF}$,求出直线的斜率.
解答  解:抛物线Γ:y2=4x的焦点F(1,0),设Q到l的距离为d,则|QF|=|AQ|=d,
解:抛物线Γ:y2=4x的焦点F(1,0),设Q到l的距离为d,则|QF|=|AQ|=d,
∵$\overrightarrow{PQ}$=3$\overrightarrow{QF}$,
∴|$\overrightarrow{PQ}$|=3d,|PA|=$\sqrt{(3d)^{2}-{d}^{2}}$=2$\sqrt{2}$d,
∵点P(x0,y0)(y0>0),
∴直线PF的斜率kPF=-$\frac{|PA|}{|AQ|}$=-$\frac{2\sqrt{2}d}{d}$=2$\sqrt{2}$,
故答案为:-2$\sqrt{2}$.
点评 本题考查抛物线的简单性质,考查直线与抛物线的位置关系,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.某课题研究小组对学生报读文科和理科的人数进行了调查统计,结果如下:
在探究学生性别与报读文科、理科是否有关时,根据以上数据可以得到K2=19.308,则( )
| 文科 | 理科 | 合计 | |
| 男生 | 52 | 98 | 150 |
| 女生 | 90 | 60 | 150 |
| 合计 | 42 | 158 | 300 |
| A. | 学生的性别与是否报读文科、理科有关 | |
| B. | 学生的性别与是否报读文科、理科无关 | |
| C. | 在犯错误的概率不超过0.001的前提下认为学生的性别与是否报读文科、理科有关 | |
| D. | 在犯错误的概率不超过0.001的前提下认为学生的性别与是否报读文科、理科无关 |
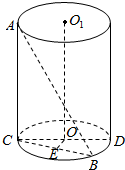 如图,AC为圆柱的母线,CD为底面直径,线段AB的两个端点分别在上、下底面圆周上,它与圆周的轴OO1之间的距离为3,所成角为30°,且AB=16,求此圆柱的侧面积.
如图,AC为圆柱的母线,CD为底面直径,线段AB的两个端点分别在上、下底面圆周上,它与圆周的轴OO1之间的距离为3,所成角为30°,且AB=16,求此圆柱的侧面积.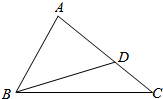 如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.
如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.