题目内容
17.已知{an}是等差数列,点(an,bn)在函数f(x)=2x的图象上(n∈N*),且a1=0,函数f(x)的图象在点(a2,b2)处切线的横截距为1-$\frac{1}{ln2}$.(1)求数列{an}、{bn}的通项公式;
(2)若数列{bn}的前n项和为Sn,cn+1=(-1)n+1cn+Sn,c1=2,求数列{cn}的前40项的和.
分析 (1)通过对f(x)=2x求导可知f'(x)=2xln2,进而可知切线方程为y-b2=(${2}^{{a}_{2}}$ln2)(x-a2),通过解方程a2-$\frac{{b}_{2}}{{2}^{{a}_{2}}ln2}$=1-$\frac{1}{ln2}$可知a2=1,进而计算可得结论;
(2)通过(1)可知Sn=2n-1,从cn+1=(-1)n+1cn+Sn,进而C4n+1=C4n+1、C4n+2=C4n+1+S4n+1、C4n+3=-C4n+1-S4n+1+S4n+2、C4n+4=-C4n+1-S4n+1+S4n+2+S4n+3,计算可知dn=C4n+1+C4n+2+C4n+3+C4n+4=-2+14•24n,计算即得结论.
解答 解:(1)由f(x)=2x得f'(x)=2xln2,
∴函数f(x)的图象在点(a2,b2)处的切线斜率k=f′(a2)=${2}^{{a}_{2}}$ln2,
从而切线方程为y-b2=(${2}^{{a}_{2}}$ln2)(x-a2),
∴切线在x轴上的截距为a2-$\frac{{b}_{2}}{{2}^{{a}_{2}}ln2}$,
从而a2-$\frac{{b}_{2}}{{2}^{{a}_{2}}ln2}$=a2-$\frac{{b}_{2}}{{b}_{2}ln2}$=a2-$\frac{1}{ln2}$=1-$\frac{1}{ln2}$,
∴a2=1,
∴公差d=a2-a1=1-0=1,
∴数列{an}的通项公式为an=a1+(n-1)d=n-1;
∴数列{bn}的通项公式为bn=${2}^{{a}_{n}}$=2n-1;
(2)由(1)可知Sn=$\frac{1-{2}^{n}}{1-2}$=2n-1,
∴cn+1=(-1)n+1cn+Sn=(-1)n+1cn+2n-1,
∴C4n+1=C4n+1,
C4n+2=C4n+1+S4n+1,
C4n+3=-C4n+2+S4n+2=-C4n+1-S4n+1+S4n+2,
C4n+4=C4n+3+S4n+3=-C4n+1-S4n+1+S4n+2+S4n+3,
令dn=C4n+1+C4n+2+C4n+3+C4n+4
=C4n+1+(C4n+1+S4n+1)+(-C4n+1-S4n+1+S4n+2)+(-C4n+1-S4n+1+S4n+2+S4n+3)
=-S4n+1+2S4n+2+S4n+3
=-(24n+1-1)+2(24n+2-1)+24n+3-1
=-2+14•24n,
∴所求值为d0+d1+d2+…+d9
=-20+14(20+24+28+…+236)
=-20+14•$\frac{1-{2}^{40}}{1-{2}^{4}}$
=-20+$\frac{14}{15}$•(240-1).
点评 本题考查等差数列的概念,前n项和公式,导数的几何意义等知识;考查学生的运算求解能力、推理论证能力,注意解题方法的积累,属于难题.

 特高级教师点拨系列答案
特高级教师点拨系列答案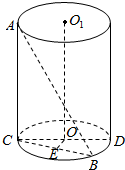 如图,AC为圆柱的母线,CD为底面直径,线段AB的两个端点分别在上、下底面圆周上,它与圆周的轴OO1之间的距离为3,所成角为30°,且AB=16,求此圆柱的侧面积.
如图,AC为圆柱的母线,CD为底面直径,线段AB的两个端点分别在上、下底面圆周上,它与圆周的轴OO1之间的距离为3,所成角为30°,且AB=16,求此圆柱的侧面积.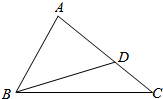 如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.
如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.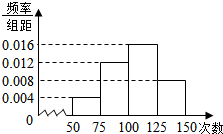 为了解初中生的身体素质,某地随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第2小组的频数是36,则n的值为120.
为了解初中生的身体素质,某地随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第2小组的频数是36,则n的值为120.