题目内容
13．求下列函数的定义域：（1）y=$\frac{（x+2）^{2}}{|x|-x}$；
（2）f（x）=$\frac{{x}^{2}-1}{x-1}$-$\sqrt{4-x}$．
分析 （1）利用分母不为0，求解函数的定义域．
（2）利用分母不为0，开偶次方被开方数非负，可得不等式组求解即可得到函数的定义域．
解答 解：（1）要使函数有意义，必有：|x|-x≠0，解得x＜0，
所以函数的定义域为：{x|x＜0}．
（2）要使函数有意义，则$\left\{\begin{array}{l}x-1≠0\\ 4-x≥0\end{array}\right.$，解得x≤4且x≠1．
所以函数的定义域为：{x|x≤4且x≠1}．
点评 b本题考查函数的定义域的求法，基本知识的考查．
练习册系列答案
相关题目
18．函数y=$\frac{\sqrt{1-x}}{2{x}^{2}-3x-2}$的定义域是（ ）
| A． | （-∞，1] | B． | （-∞，2] | C． | （-∞，-$\frac{1}{2}$）∪（-$\frac{1}{2}$，2） | D． | （-∞，-$\frac{1}{2}$）∪（-$\frac{1}{2}$，1] |
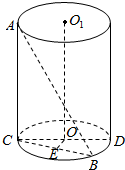如图，AC为圆柱的母线，CD为底面直径，线段AB的两个端点分别在上、下底面圆周上，它与圆周的轴OO1之间的距离为3，所成角为30°，且AB=16，求此圆柱的侧面积．