题目内容

18．已知集合A={1，3，x3}，B={x+2，1}，是否存在实数x，使得B⊆A？若存在，求出集合A，B；若不存在，请说明理由．

分析 可假设B⊆A，这样便有x+2=3，或x+2=-x3，这样解出x，从而得出A，B，判断是否满足B⊆A即可．

解答 解：若B⊆A，则：
x+2=3，或x+2=-x3；
（1）x+2=3时，x=1；
∴A={1，3，-1}，B={3，1}，满足B⊆A；
（2）x+2=x3时，x3-x-2=（x3+1）+（x+1）=（x+1）（x2-x+2）=0，x=-1；
此时B={1，1}，不满足集合元素的互异性，即x≠-1；
∴存在实数x=1，使得B是A的子集，且A={1，3，-1}，B={3，1}．

点评 考查列举法表示集合，子集的定义，以及集合元素的互异性，立方和公式．

练习册系列答案
相关题目
8．已知函数y=f（x）的定义域是[1，4]，则函数y=f（x+1）的定义域是[0，3]．
9．若函数f（x）的定义域是[0，4]，则函数g（x）=$\frac{f（x+1）}{x}$的定义域是（　　）
A．[0，3]B．（-1，3）C．[-1，0）∪（0，3]D．（-1，3]
6．己知函数f（x）=logax（a＞0，且a≠1），若x＜0时，有ax＞1，则不等式f（1-$\frac{1}{x}$）＞1的解集为（1，$\frac{1}{1-a}$）．
13．已知数列{an}的通项公式为an=25-2n，在下列各数中，不是{an}的项的是（　　）
A．1B．-1C．3D．2
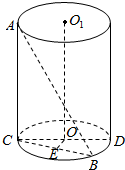5．如图，AC为圆柱的母线，CD为底面直径，线段AB的两个端点分别在上、下底面圆周上，它与圆周的轴OO1之间的距离为3，所成角为30°，且AB=16，求此圆柱的侧面积．
12．若数列{an}是公差为正数的等差数列，且对任意n∈N*有an•Sn=2n3-n2．
（1）求数列{an}的通项公式；
（2）是否存在数列{bn}，使得数列{anbn}的前n项和为An=5+（2n-3）2n-1（n∈N*）？若存在，求出数列{bn}的通项公式及前n项和Tn；若不存在，请说明理由．
9．设[x]表示不超过x的最大整数（如[2]=2，[$\frac{5}{4}$]=1），对于给定的n∈N*，定义${C}_{n}^{x}$=$\frac{n（n-1）…（n-[x]+1）}{x（x-1）…（x-[x]+1）}$，x∈[1，+∞），当x∈[3，4）时，函数${C}_{8}^{x}$的值域为（14，56]．
10．已知函数f（x）=-sin2x+sinx+$\frac{1}{2}$，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]．
（1）求函数f（x）的值域；
（2）设函数g（x）=acosx-2，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]，若对于任意x1∈[-$\frac{π}{2}$，$\frac{π}{2}$]，一定存在x0∈[-$\frac{π}{2}$，$\frac{π}{2}$]，使得g（x0）=f（x1）成立，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网